Resources

Testimonials

Plans

Resources

Testimonials

Plans

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

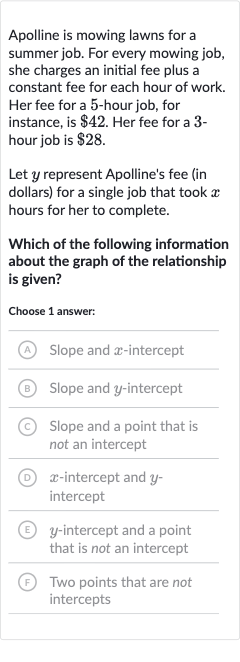
Apolline is mowing lawns for a summer job. For every mowing job, she charges an initial fee plus a constant fee for each hour of work. Her fee for a $5$ -hour job, for instance, is $\$ 42$ . Her fee for a $3$ hour job is $\$ 28$ . $\newline$ Let $y$ represent Apolline's fee (in dollars) for a single job that took $x$ hours for her to complete. $\newline$ Which of the following information about the graph of the relationship is given? $\newline$ Choose $1$ answer: $\newline$ (A) Slope and $x$ -intercept $\newline$ (B) Slope and $y$ -intercept $\newline$ (C) Slope and a point that is not an intercept $\newline$ (D) $x$ -intercept and $y$ intercept $\newline$ (E) $y$ -intercept and a point that is not an intercept $\newline$ (F) Two points that are not intercepts

View step-by-step help

Home

Math Problems

Algebra 2

Write equations of sine and cosine functions using properties

Full solution

Q. Apolline is mowing lawns for a summer job. For every mowing job, she charges an initial fee plus a constant fee for each hour of work. Her fee for a

5

-hour job, for instance, is

\$ 42

. Her fee for a

3

hour job is

\$ 28

\newline

Let

y

represent Apolline's fee (in dollars) for a single job that took

x

hours for her to complete.

\newline

Which of the following information about the graph of the relationship is given?

\newline

Choose

1

answer:

\newline

(A) Slope and

x

-intercept

\newline

(B) Slope and

y

-intercept

\newline

\newline

(D)

x

-intercept and

y

intercept

\newline

(E)

y

-intercept and a point that is not an intercept

\newline

(F) Two points that are not intercepts

Define Variables: Let's denote the initial fee that Apolline charges as $b$ (which will be the y-intercept of the graph) and the constant fee per hour as $m$ (which will be the slope of the graph). We can then express Apolline's fee for a job as $y = mx + b$ , where $y$ is the total fee and $x$ is the number of hours worked.
Calculate Slope: We are given two points: ( $5$ , $42$ ) for a $5$ -hour job and ( $3$ , $28$ ) for a $3$ -hour job. These points can be used to find the slope $m$ of the graph. The slope $m$ is calculated by the change in $y$ divided by the change in $x$ , which is $(42 - 28) / (5 - 3)$ .
Find Y-Intercept: Performing the calculation for the slope $m$ , we get $m = (42 - 28) / (5 - 3) = 14 / 2 = 7$ . So, Apolline charges $7$ per hour of work.
Determine Initial Fee: Now that we have the slope $ m $, we can use one of the points to find the y-intercept $ b $. Let's use the point ($5$, $42$). Plugging these values into the equation $ y = mx + b $, we get $ 42 = 7(5) + b $.
Describe Graph: Solving for $ b $, we have $ 42 = 35 + b $, which gives us $ b = 42 - 35 = 7 $. Therefore, the initial fee that Apolline charges is $7$ .
Identify Given Information: With the slope $m = 7$ and the y-intercept $b = 7$ , we have enough information to describe the graph of the relationship. The slope corresponds to the constant fee per hour, and the y-intercept corresponds to the initial fee.
Identify Given Information: With the slope $m = 7$ and the y-intercept $b = 7$ , we have enough information to describe the graph of the relationship. The slope corresponds to the constant fee per hour, and the y-intercept corresponds to the initial fee.The question asks which of the following information about the graph is given. We have determined both the slope and the y-intercept from the information provided. Therefore, the correct answer is (B) Slope and y-intercept.