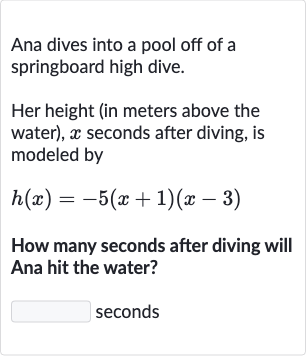
Ana dives into a pool off of a springboard high dive. Her height (in meters above the water), x seconds after diving, is modeled by h(x)=-5(x+1)(x-3) How many seconds after diving will Ana hit the water? seconds

Question

Ana dives into a pool off of a springboard high dive. Her height (in meters above the water),  x seconds after diving, is modeled by  h(x)=-5(x+1)(x-3) How many seconds after diving will Ana hit the water? seconds

Bytelearn · Accepted Answer

Set Equation to Zero: We need to find the value of x for which Ana's height above the water is zero, i.e., h(x) = 0. h(x) = -5(x+1)(x-3) Set h(x) to zero and solve for x: 0 = -5(x+1)(x-3)Simplify Equation: Divide both sides of the equation by -5 to simplify the equation: 0 = (x+1)(x-3)Quadratic Equation in Factored Form: Now we have a quadratic equation in factored form. Set each factor equal to zero and solve for x: x+1 = 0 or x-3 = 0Solve for x: Solve the first equation for x: x+1 = 0 x = -1Discard Negative Value: Solve the second equation for x: x-3 = 0 x = 3Final Solution: We have two solutions for x: x = -1 and x = 3. Since time cannot be negative in this context, we discard the negative value. Therefore, Ana will hit the water 3 seconds after diving.

Ana dives into a pool off of a springboard high dive. Her height (in meters above the water), $x$ seconds after diving, is modeled by $\newline$ $h(x) = -5(x+1)(x-3)$ $\newline$ How many seconds after diving will Ana hit the water? $\newline$ $\text{seconds}$

Full solution

More problems from Find the roots of factored polynomials

Related topics