Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

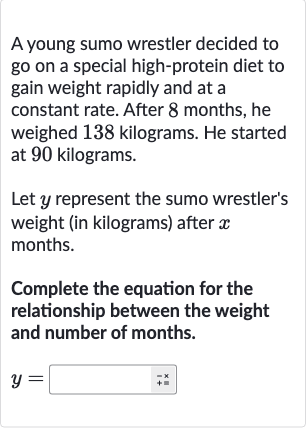
A young sumo wrestler decided to go on a special high-protein diet to gain weight rapidly and at a constant rate. After 8 months, he weighed 138 kilograms. He started at 90 kilograms. Let y represent the sumo wrestler's weight (in kilograms) after x months. Complete the equation for the relationship between the weight and number of months. y=

A young sumo wrestler decided to go on a special high-protein diet to gain weight rapidly and at a constant rate. After 88 months, he weighed 138138 kilograms. He started at 9090 kilograms.\newlineLet y y represent the sumo wrestler's weight (in kilograms) after x x months.\newlineComplete the equation for the relationship between the weight and number of months.\newliney=□ y=\square

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Write exponential functions: word problemsright chevron icon

Full solution

Q. A young sumo wrestler decided to go on a special high-protein diet to gain weight rapidly and at a constant rate. After 88 months, he weighed 138138 kilograms. He started at 9090 kilograms.\newlineLet y y represent the sumo wrestler's weight (in kilograms) after x x months.\newlineComplete the equation for the relationship between the weight and number of months.\newliney=□ y=\square
  1. Determining the rate of weight gain: First, let's determine the rate of weight gain per month.\newlineThe sumo wrestler started at 9090 kilograms and after 88 months weighed 138138 kilograms.\newlineTo find the rate of weight gain, we subtract the starting weight from the final weight and then divide by the number of months.\newlineRate of weight gain per month = Final weight−Starting weightNumber of months\frac{\text{Final weight} - \text{Starting weight}}{\text{Number of months}}\newlineRate of weight gain per month = 138 kg−90 kg8 months\frac{138 \text{ kg} - 90 \text{ kg}}{8 \text{ months}}\newlineRate of weight gain per month = 48 kg8 months\frac{48 \text{ kg}}{8 \text{ months}}\newlineRate of weight gain per month = 66 kg/month
  2. Writing the equation for the sumo wrestler's weight: Now that we have the rate of weight gain, we can write the equation for the sumo wrestler's weight after xx months.\newlineThe equation will be in the form of a linear equation y=mx+by = mx + b, where mm is the rate of weight gain per month, and bb is the starting weight.\newlineSince we know the rate of weight gain is 6 kg/month6\,\text{kg/month} and the starting weight is 90 kg90\,\text{kg}, the equation is:\newliney=6x+90y = 6x + 90
  3. Checking the equation with the given data: Let's check the equation with the given data to ensure there are no math errors.\newlineIf we substitute x=8x = 8 months into the equation, we should get the sumo wrestler's weight after 88 months, which is 138138 kg.\newliney=6(8)+90y = 6(8) + 90\newliney=48+90y = 48 + 90\newliney=138y = 138 kg\newlineThis matches the given information, so the equation is correct.

More problems from Write exponential functions: word problems

Question
Use the following function rule to find f(2) f(2) .\newlinef(x)=11⋅(9)x+8 f(x) = 11 \cdot (9)^x + 8 \newlinef(2)= f(2) = _____
Get tutor helpright-arrow

Posted 5 months ago

Question
Raymond works for a pharmaceutical company that is testing the effectiveness of a new medication. He gave one of the study participants 400400 milligrams of the medication, and he knows the amount remaining in the participant's body will decrease by a factor of 1/31/3 each hour.\newlineWrite an exponential equation in the form y=a(b)xy = a(b)^x that can model the amount of medication, yy, remaining in the participant's body after xx hours.\newlineUse whole numbers, decimals, or simplified fractions for the values of aa and bb.\newliney=y = ______\newline
Get tutor helpright-arrow

Posted 8 months ago

Question
A colony of 100100 bacteria doubles in size every 6060 hours. What will the population be 180180 hours from now??
Get tutor helpright-arrow

Posted 4 months ago

Question
Charlotte opened a savings account and deposited $800.00\$800.00 as principal. The account earns 8%8\% interest, compounded annually. What is the balance after 1010 years?\newlineUse the formula A=P(1+rn)ntA = P(1 + \frac{r}{n})^{nt}, where AA is the balance (final amount), PP is the principal (starting amount), rr is the interest rate expressed as a decimal, nn is the number of times per year that the interest is compounded, and tt is the time in years.\newlineRound your answer to the nearest cent.
Get tutor helpright-arrow

Posted 4 months ago

Question
Bob rented a car for a flat fee of `$150` and an additional `$10` per day. Write a linear function that represents the total cost, f(x)f(x), after xx days.
Get tutor helpright-arrow

Posted 10 months ago

Question
Sally purchased a laptop for `$800` and has to pay a service fee of `$20` for each day until it is delivered. Write a linear function to represent the total cost, h(x)h(x), after xx days.
Get tutor helpright-arrow

Posted 10 months ago

Question
Kevin invested $1,000\$1,000 in a savings account with a daily interest rate of 0.1%0.1\%. Write an exponential function to represent the total amount, s(x)s(x), in his account after xx days.
Get tutor helpright-arrow

Posted 9 months ago

Question
A=2450+740s A=2450+740 s \newlineThe total amount, A A , in thousands of dollars, of scholarship money given out by a college throughout its history at a time of s s semesters after the summer of the year 20002000 is given by the equation. What was the total amount of scholarship money, in thousands of dollars, given out by the college up to the summer of the year 20002000 ?
Get tutor helpright-arrow

Posted 5 months ago

Question
T=235+980d T=235+980 d \newlineThe torque, T T , in newton-meters, on a diving board with a 100100 kilogram weight placed d d meters from the diving board's fulcrum is given by the equation. How much torque in newton-meters is on the diving board when the weight is placed at the fulcrum?
Get tutor helpright-arrow

Posted 8 months ago

Question
R=42−0.7t R=42-0.7 t \newlineQuinn returned home one summer's day to find it extremely hot. He turned the air conditioner on, and the room's temperature began decreasing at a constant rate. The given equation shown gives the room's temperature, R R , in degrees Celsius, t t minutes after Quinn turned on the air conditioner. What was the room's temperature, in degrees Celsius, when Quinn returned home?
Get tutor helpright-arrow

Posted 7 months ago

View all (82)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant