Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

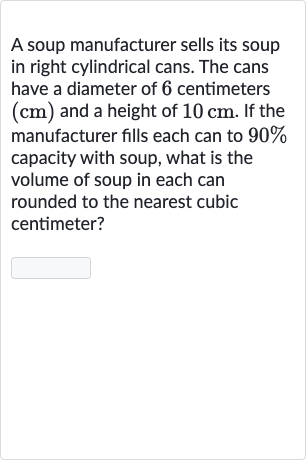
A soup manufacturer sells its soup in right cylindrical cans. The cans have a diameter of 6 centimeters (cm) and a height of 10cm. If the manufacturer fills each can to 90% capacity with soup, what is the volume of soup in each can rounded to the nearest cubic centimeter?

A soup manufacturer sells its soup in right cylindrical cans. The cans have a diameter of 66 centimeters (cm) (\mathrm{cm}) and a height of 10 cm 10 \mathrm{~cm} . If the manufacturer fills each can to 90% 90 \% capacity with soup, what is the volume of soup in each can rounded to the nearest cubic centimeter?

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Weighted averages: word problemsright chevron icon

Full solution

Q. A soup manufacturer sells its soup in right cylindrical cans. The cans have a diameter of 66 centimeters (cm) (\mathrm{cm}) and a height of 10 cm 10 \mathrm{~cm} . If the manufacturer fills each can to 90% 90 \% capacity with soup, what is the volume of soup in each can rounded to the nearest cubic centimeter?
  1. Calculate total volume of cylindrical can: First, we need to calculate the total volume of the cylindrical can. The formula for the volume of a cylinder is V=πr2hV = \pi r^2 h, where rr is the radius and hh is the height.\newlineGiven the diameter of the can is 6 cm6 \, \text{cm}, the radius rr is half of that, which is 3 cm3 \, \text{cm}. The height hh is given as 10 cm10 \, \text{cm}.\newlineNow we calculate the volume: \newlineV=π×(3 cm)2×10 cmV = \pi \times (3 \, \text{cm})^2 \times 10 \, \text{cm}
  2. Perform volume calculation: Perform the calculation for the volume: \newlineV=π×9 cm2×10 cm=90π cm3V = \pi \times 9 \text{ cm}^2 \times 10 \text{ cm} = 90\pi \text{ cm}^3 \newlineSince π\pi is approximately 3.141593.14159, we can calculate the volume as: \newlineV≈90×3.14159 cm3V \approx 90 \times 3.14159 \text{ cm}^3.
  3. Calculate 9090% of total volume: Now we have the total volume of the can: \newlineV≈282.74 cm3V \approx 282.74\,\text{cm}^3 (rounded to two decimal places for intermediate calculation).\newlineNext, we need to calculate 9090% of this volume to find out how much soup the manufacturer fills in each can.\newline9090% of the total volume is 0.9×282.74 cm30.9 \times 282.74\,\text{cm}^3.
  4. Round to nearest cubic centimeter: Perform the calculation for 9090% of the volume: \newline0.9×282.74 cm3≈254.47 cm30.9 \times 282.74 \, \text{cm}^3 \approx 254.47 \, \text{cm}^3 \newlineWe need to round this to the nearest cubic centimeter.
  5. Final volume of soup in each can: Rounding 254.47 cm3254.47 \, \text{cm}^3 to the nearest cubic centimeter gives us 254 cm3254 \, \text{cm}^3. This is the volume of soup in each can when filled to 90%90\% capacity.

More problems from Weighted averages: word problems

Question
Eric made a scale drawing of the auditorium. The stage, which is \(35\) feet wide in real life, is \(5\) inches wide in the drawing. What is the scale of the drawing? \(1\) inch : _____\_\_\_\_\_ feet
Get tutor helpright-arrow

Posted 5 months ago

Question
Convert.\newline6666 cups==_____\_\_\_\_\_ fluid ounces
Get tutor helpright-arrow

Posted 5 months ago

Question
Convert.\newline1,0001,000 milligrams\text{ milligrams}=____\_\_\_\_ grams\text{ grams}
Get tutor helpright-arrow

Posted 5 months ago

Question
A 33-gallon bottle of bleach costs $11.52\$11.52. What is the price per quart?\newline`$`_____
Get tutor helpright-arrow

Posted 5 months ago

Question
Maureen can't wait to make chocolate chip zucchini bread with zucchini from her garden. Her recipe calls for 88 ounces of chocolate chips per loaf. If she has enough zucchini to make 44 loaves of zucchini bread, how many pounds of chocolate chips does she need?\newlineHint: There are 1616 ounces in 11 pound.\newlineWrite your answer as a whole number, decimal, or simplified fraction. Do not round.\newline____ pounds
Get tutor helpright-arrow

Posted 5 months ago

Question
A whale is swimming due north at a speed of 3030 miles per hour. Just 55 miles away, a whale-watching tour boat is traveling south, directly toward the whale, at a speed of 4646 miles per hour. How long will it be before they meet? If necessary, round your answer to the nearest minute. ____\_\_\_\_ hours and ____\_\_\_\_ minutes
Get tutor helpright-arrow

Posted 5 months ago

Question
Wyatt, a chemist at a chemical supply company, has carefully measured out 100100 gallons of a solution containing 14%14\% acetone. He also has access to unlimited quantities of a 9%9\% acetone solution. How many gallons of the 9%9\% acetone solution must Wyatt add to the 14%14\% acetone solution to create a solution that contains 10%10\% acetone?\newlineWrite your answer as a whole number or as a decimal rounded to the nearest tenth.\newline\newline____ gallons\newline
Get tutor helpright-arrow

Posted 5 months ago

Question
William recently started running after school. Yesterday, he ran 4.84.8 miles in 4141 minutes and 66 seconds. Today, he ran 4.14.1 miles in 3333 minutes and 44 seconds. What was William's average speed over the two runs?\newlineWrite your answer as a whole number, a decimal, or a simplified fraction or mixed number. Do not round.\newline\newline____ miles per minute\newline
Get tutor helpright-arrow

Posted 7 months ago

Question
Convert.\newline750750 milligrams== _____ grams
Get tutor helpright-arrow

Posted 7 months ago

Question
Convert. \newline250250 milligrams == _____ grams
Get tutor helpright-arrow

Posted 7 months ago

View all (54)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant