AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
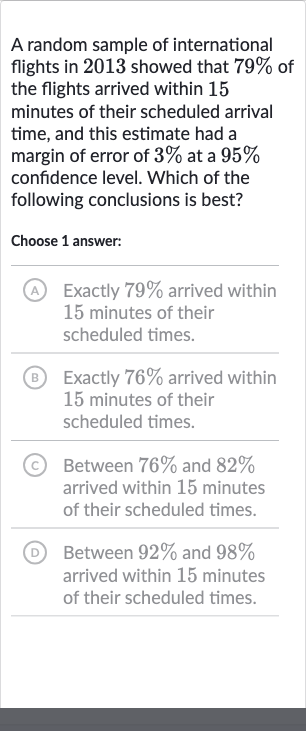
A random sample of international flights in showed that of the flights arrived within minutes of their scheduled arrival time, and this estimate had a margin of error of at a confidence level. Which of the following conclusions is best?Choose answer:(A) Exactly arrived within minutes of their scheduled times.(B) Exactly arrived within minutes of their scheduled times.(C) Between and arrived within minutes of their scheduled times.(D) Between and arrived within minutes of their scheduled times.
Full solution
Q. A random sample of international flights in showed that of the flights arrived within minutes of their scheduled arrival time, and this estimate had a margin of error of at a confidence level. Which of the following conclusions is best?Choose answer:(A) Exactly arrived within minutes of their scheduled times.(B) Exactly arrived within minutes of their scheduled times.(C) Between and arrived within minutes of their scheduled times.(D) Between and arrived within minutes of their scheduled times.
- Problem statement: The problem states that of the flights arrived within minutes of their scheduled arrival time with a margin of error of at a confidence level. To find the range, we need to add and subtract the margin of error from the estimated percentage.
- Calculate lower bound: Calculate the lower bound of the confidence interval by subtracting the margin of error from the estimated percentage.Lower bound = Estimated percentage - Margin of errorLower bound = Lower bound =
- Calculate upper bound: Calculate the upper bound of the confidence interval by adding the margin of error to the estimated percentage.Upper bound = Estimated percentage + Margin of errorUpper bound = Upper bound =
- Determine range: Now we have the range for the confidence interval.The range is from to .
- Compare with options: Compare the range with the given options to determine the best conclusion.Option (C) states "Between and arrived within minutes of their scheduled times," which matches our calculated range.
More problems from Interpret confidence intervals for population means
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
