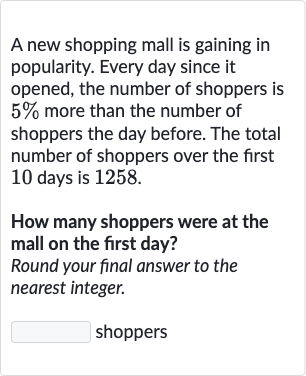
A new shopping mall is gaining in popularity. Every day since it opened, the number of shoppers is 5% more than the number of shoppers the day before. The total number of shoppers over the first 10 days is 1258 . How many shoppers were at the mall on the first day? Round your final answer to the nearest integer. shoppers

Question

A new shopping mall is gaining in popularity. Every day since it opened, the number of shoppers is  5% more than the number of shoppers the day before. The total number of shoppers over the first 10 days is 1258 . How many shoppers were at the mall on the first day? Round your final answer to the nearest integer. shoppers

Bytelearn · Accepted Answer

Denote Shoppers on First Day: Let's denote the number of shoppers on the first day as $ S $. Since the number of shoppers increases by 5% each day, the number of shoppers on the second day would be $ S \times 1.05 $, on the third day $ S \times 1.05^2 $, and so on, up to the tenth day which would be $ S \times 1.05^9 $. The total number of shoppers over the first 10 days is given as 1258. We can write this as a geometric series: $$ S + S \times 1.05 + S \times 1.05^2 + \ldots + S \times 1.05^9 = 1258 $$Calculate Geometric Series: The sum of a geometric series can be calculated using the formula: $$ S \times \frac{1 - r^n}{1 - r} $$ where $ S $ is the first term, $ r $ is the common ratio (1.05 in this case), and $ n $ is the number of terms (10 in this case). We can plug in the values to find $ S $: $$ S \times \frac{1 - 1.05^{10}}{1 - 1.05} = 1258 $$Apply Geometric Series Formula: Now we solve for $ S $: $$ S \times \frac{1 - 1.05^{10}}{-0.05} = 1258 $$ $$ S \times \frac{1 - 1.628894626777442}{-0.05} = 1258 $$ $$ S \times \frac{-0.628894626777442}{-0.05} = 1258 $$ $$ S \times 12.57789253554884 = 1258 $$ $$ S = \frac{1258}{12.57789253554884} $$ $$ S \approx 100 $$Solve for S: We round the final answer to the nearest integer: $$ S \approx 100 $$

Full solution

More problems from Exponential growth and decay: word problems

Related topics