Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

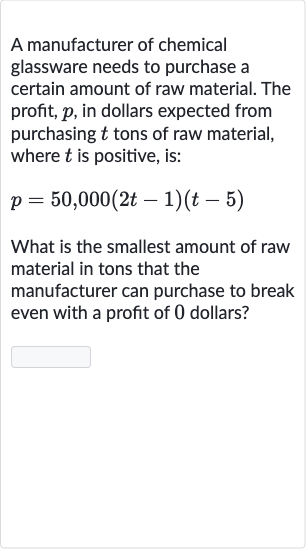
A manufacturer of chemical glassware needs to purchase a certain amount of raw material. The profit, p, in dollars expected from purchasing t tons of raw material, where t is positive, is: p=50,000(2t-1)(t-5) What is the smallest amount of raw material in tons that the manufacturer can purchase to break even with a profit of 0 dollars?

A manufacturer of chemical glassware needs to purchase a certain amount of raw material. The profit, p p , in dollars expected from purchasing t t tons of raw material, where t t is positive, is:\newlinep=50,000(2t−1)(t−5) p=50,000(2 t-1)(t-5) \newlineWhat is the smallest amount of raw material in tons that the manufacturer can purchase to break even with a profit of 00 dollars?

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Write exponential functions: word problemsright chevron icon

Full solution

Q. A manufacturer of chemical glassware needs to purchase a certain amount of raw material. The profit, p p , in dollars expected from purchasing t t tons of raw material, where t t is positive, is:\newlinep=50,000(2t−1)(t−5) p=50,000(2 t-1)(t-5) \newlineWhat is the smallest amount of raw material in tons that the manufacturer can purchase to break even with a profit of 00 dollars?
  1. Set Profit Equation: To find the smallest amount of raw material in tons that the manufacturer can purchase to break even, we need to set the profit equation pp equal to 00 and solve for tt.
    p=50,000(2t−1)(t−5)p = 50,000(2t - 1)(t - 5)
    0=50,000(2t−1)(t−5)0 = 50,000(2t - 1)(t - 5)
  2. Divide by 5050,000000: Since the profit pp is multiplied by 50,00050,000, we can divide both sides of the equation by 50,00050,000 to simplify the equation without affecting the value of tt.0=(2t−1)(t−5)0 = (2t - 1)(t - 5)
  3. Solve Quadratic Equation: Now we have a quadratic equation in factored form. To find the values of tt that make the profit zero, we set each factor equal to zero and solve for tt.\newlineFirst, set the first factor equal to zero:\newline2t−1=02t - 1 = 0
  4. First Factor Zero: Solve for tt by adding 11 to both sides and then dividing by 22:2t=12t = 1t=12t = \frac{1}{2}
  5. Second Factor Zero: Now, set the second factor equal to zero:\newlinet−5=0t - 5 = 0
  6. Valid Solutions: Solve for tt by adding 55 to both sides:\newlinet=5t = 5
  7. Compare Values: We have found two values of tt, 12\frac{1}{2} and 55. Since tt represents the tons of raw material and must be positive, both are valid solutions. However, we are looking for the smallest amount of raw material to break even.
  8. Smallest Amount: Comparing the two values, 12\frac{1}{2} ton and 55 tons, we see that 12\frac{1}{2} ton is the smaller amount. Therefore, the smallest amount of raw material the manufacturer can purchase to break even is 12\frac{1}{2} ton.

More problems from Write exponential functions: word problems

Question
Use the following function rule to find f(2) f(2) .\newlinef(x)=11⋅(9)x+8 f(x) = 11 \cdot (9)^x + 8 \newlinef(2)= f(2) = _____
Get tutor helpright-arrow

Posted 5 months ago

Question
Raymond works for a pharmaceutical company that is testing the effectiveness of a new medication. He gave one of the study participants 400400 milligrams of the medication, and he knows the amount remaining in the participant's body will decrease by a factor of 1/31/3 each hour.\newlineWrite an exponential equation in the form y=a(b)xy = a(b)^x that can model the amount of medication, yy, remaining in the participant's body after xx hours.\newlineUse whole numbers, decimals, or simplified fractions for the values of aa and bb.\newliney=y = ______\newline
Get tutor helpright-arrow

Posted 8 months ago

Question
A colony of 100100 bacteria doubles in size every 6060 hours. What will the population be 180180 hours from now??
Get tutor helpright-arrow

Posted 4 months ago

Question
Charlotte opened a savings account and deposited $800.00\$800.00 as principal. The account earns 8%8\% interest, compounded annually. What is the balance after 1010 years?\newlineUse the formula A=P(1+rn)ntA = P(1 + \frac{r}{n})^{nt}, where AA is the balance (final amount), PP is the principal (starting amount), rr is the interest rate expressed as a decimal, nn is the number of times per year that the interest is compounded, and tt is the time in years.\newlineRound your answer to the nearest cent.
Get tutor helpright-arrow

Posted 4 months ago

Question
Bob rented a car for a flat fee of `$150` and an additional `$10` per day. Write a linear function that represents the total cost, f(x)f(x), after xx days.
Get tutor helpright-arrow

Posted 10 months ago

Question
Sally purchased a laptop for `$800` and has to pay a service fee of `$20` for each day until it is delivered. Write a linear function to represent the total cost, h(x)h(x), after xx days.
Get tutor helpright-arrow

Posted 10 months ago

Question
Kevin invested $1,000\$1,000 in a savings account with a daily interest rate of 0.1%0.1\%. Write an exponential function to represent the total amount, s(x)s(x), in his account after xx days.
Get tutor helpright-arrow

Posted 9 months ago

Question
A=2450+740s A=2450+740 s \newlineThe total amount, A A , in thousands of dollars, of scholarship money given out by a college throughout its history at a time of s s semesters after the summer of the year 20002000 is given by the equation. What was the total amount of scholarship money, in thousands of dollars, given out by the college up to the summer of the year 20002000 ?
Get tutor helpright-arrow

Posted 5 months ago

Question
T=235+980d T=235+980 d \newlineThe torque, T T , in newton-meters, on a diving board with a 100100 kilogram weight placed d d meters from the diving board's fulcrum is given by the equation. How much torque in newton-meters is on the diving board when the weight is placed at the fulcrum?
Get tutor helpright-arrow

Posted 8 months ago

Question
R=42−0.7t R=42-0.7 t \newlineQuinn returned home one summer's day to find it extremely hot. He turned the air conditioner on, and the room's temperature began decreasing at a constant rate. The given equation shown gives the room's temperature, R R , in degrees Celsius, t t minutes after Quinn turned on the air conditioner. What was the room's temperature, in degrees Celsius, when Quinn returned home?
Get tutor helpright-arrow

Posted 7 months ago

View all (82)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant