Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

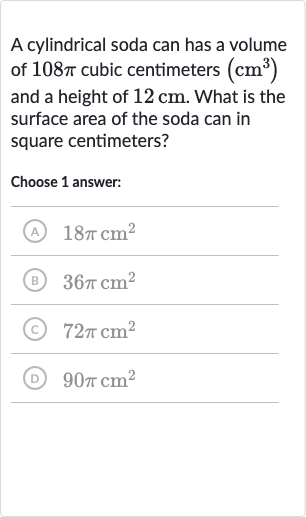
A cylindrical soda can has a volume of
108 pi cubic centimeters
(cm^(3)) and a height of
12cm. What is the surface area of the soda can in square centimeters?
Choose 1 answer:
(A)
18 picm^(2)
(B)
36 picm^(2)
(c)
72 picm^(2)
(D)
90 picm^(2)

A cylindrical soda can has a volume of $108 \pi$ cubic centimeters $\left(\mathrm{cm}^{3}\right)$ and a height of $12 \mathrm{~cm}$ . What is the surface area of the soda can in square centimeters? $\newline$ Choose $1$ answer: $\newline$ (A) $18 \pi \mathrm{cm}^{2}$ $\newline$ (B) $36 \pi \mathrm{cm}^{2}$ $\newline$ (C) $72 \pi \mathrm{cm}^{2}$ $\newline$ (D) $90 \pi \mathrm{cm}^{2}$

View step-by-step help

View step-by-step help

Scale drawings: word problems

Full solution

Q. A cylindrical soda can has a volume of

108 \pi

cubic centimeters

\left(\mathrm{cm}^{3}\right)

and a height of

12 \mathrm{~cm}

. What is the surface area of the soda can in square centimeters?

\newline

Choose

1

answer:

\newline

(A)

18 \pi \mathrm{cm}^{2}

\newline

(B)

36 \pi \mathrm{cm}^{2}

\newline

(C)

72 \pi \mathrm{cm}^{2}

\newline

(D)

90 \pi \mathrm{cm}^{2}

Identify Given Information: Identify the given information and the formula for the volume of a cylinder. $\newline$ Volume of a cylinder $V = \pi r^2 h$ , where $r$ is the radius and $h$ is the height. $\newline$ Given volume $V = 108\pi \, \text{cm}^3$ and height $h = 12 \, \text{cm}$ . $\newline$ We need to find the radius $r$ first.
Volume Formula Calculation: Use the volume formula to solve for the radius $r$ . $108\pi = \pi r^2(12)$ Divide both sides by $\pi$ to simplify. $108 = r^2(12)$
Radius Calculation: Divide both sides by $12$ to solve for $r^2$ . $\newline$ $\frac{108}{12} = r^2$ $\newline$ $9 = r^2$
Surface Area Formula: Take the square root of both sides to find $r$ . $\newline$ $\sqrt{9} = r$ $\newline$ $3 \, \text{cm} = r$ $\newline$ Now we have the radius of the cylinder.
Substitute Values: Identify the formula for the surface area of a cylinder. $\newline$ Surface area (SA) = $2\pi rh + 2\pi r^2$ , where the first term is the lateral surface area and the second term is the area of the two bases (top and bottom).
Simplify Expression: Substitute the known values into the surface area formula. $\newline$ $SA = 2\pi(3)(12) + 2\pi(3)^2$ $\newline$ $SA = 2\pi(36) + 2\pi(9)$
Match Correct Answer: Simplify the expression to find the surface area. $\newline$ $SA = 72\pi + 18\pi$ $\newline$ $SA = 90\pi$ cm $^2$
Match Correct Answer: Simplify the expression to find the surface area. $\newline$ $SA = 72\pi + 18\pi$ $\newline$ $SA = 90\pi \, \text{cm}^2$ Match the calculated surface area with the given answer choices. $\newline$ The correct answer is (D) $90\pi \, \text{cm}^2$ .

More problems from Scale drawings: word problems

Question

A factory designs cylindrical cans

10 \mathrm{~cm}

in height to hold exactly

500 \mathrm{~cm}^{3}

of liquid. Which of the following best approximates the radius of these cans?

\newline

1

\newline

4 \mathrm{~cm}

\newline

8 \mathrm{~cm}

\newline

12.5 \mathrm{~cm}

\newline

15.9 \mathrm{~cm}

Posted 2 months ago

Question

A die is created by smoothing the corners of a plastic cube and carving indented pips. The original cube had an edge length of

2

(\mathrm{cm})

. The volume of the final die is

7.5 \mathrm{~cm}^{3}

. What is the volume of the waste generated by creating the die from the cube in

\mathrm{cm}^{3}

Posted 23 days ago

Question

We want to find the intersection points of the graphs given by the following system of equations:

\newline

\left\{\begin{array}{l} y=2 x-1 \\ x^{2}+y^{2}=1 \end{array}\right.

\newline

One of the intersection points is

(0,-1)

\newline

Find the other intersection point. Your answer must be exact.

Posted 2 months ago

Question

A(x)=(8+2 x)^{2}

\newline

Carmen wants to add a border around a square picture. The function shows the area of the picture in square inches if it has a border

x

inches wide. What are the dimensions of the picture without the border?

\newline

1

\newline

2

2

\newline

6

6

\newline

8

8

\newline

10

10

Posted 4 months ago

Question

s=-11.8(t-1.2)^{2}+17

\newline

The equation models the horizontal distance,

s

, in centimeters, of a particular image on a computer screen from the left-hand edge of the screen,

t

seconds after appearing. If the image moves in from the left-hand edge of the screen during an on-screen animation, how far to the right does the image travel?

\newline

1

\newline

1

2

\newline

5

2

\newline

17

\newline

34

Posted 4 months ago

Question

A soap company changes the design of its soap from a cone to a sphere. The cone had a height of

3

(\mathrm{cm})

and a radius of

2 \mathrm{~cm}

. The sphere has a diameter of

3 \mathrm{~cm}

. The new design contains

\frac{\pi}{f}

cubic centimeters more soap than the old design. What is the value of

f

Posted 1 month ago

Question

Mindy is a sculptor. She has a cylinder of stone with a radius of

3

(\mathrm{m})

and a height of

2 \mathrm{~m}

. She needs to carve out a sphere of radius

1 \mathrm{~m}

from the cylinder. Mindy must cut away

\frac{v}{3} \pi

\left(\mathrm{m}^{3}\right)

of stone from the cylinder in order to be left with the sphere. What is the value of

v

Posted 1 month ago

Question

\mathrm{Cleo}

are looking for a location to open their new yoga studio. A fellow studio owner suggests a location that will fit

28

756

square foot area. Assuming that each student has a spot

x

3

times as long, what is the length, in feet, of the space they are allotting to each student?

\newline

1

\newline

1

\newline

3

\newline

9

\newline

27

Posted 1 month ago

Question

Morgan is designing a rectangular quilt. The quilt will be

1 \frac{3}{5} \mathrm{~m}

wide and will have an area of

6 \mathrm{~m}^{2}

\newline

How long is the quilt?

\newline

Posted 2 months ago

Question

Jacque needs to buy some pizzas for a party at her office. She's ordering from a restaurant that charges a

d

delivery fee and

p

per pizza. She wants to buy as many pizzas as she can, and she also needs to keep the delivery fee plus the cost of the pizzas under

T

. Each pizza is cut into

s

slices, and she wonders how many total slices she can afford. Let

n

represent the number of pizzas that Jacque buys.

\newline

1

) Which inequality describes this scenario? Choose

1

\newline

(Choice A, Checked)

A

\newline

B

\newline

C

\newline

D

\newline

2

) What is the largest number of slices that Jacque can afford?

Posted 15 hours ago