Full solution
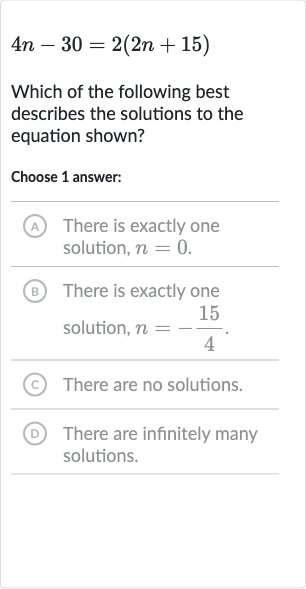
Q. Which of the following best describes the solutions to the equation shown?Choose answer:(A) There is exactly one solution, .(B) There is exactly one solution, .(C) There are no solutions.(D) There are infinitely many solutions.
- Expand and Simplify: First, we need to simplify and solve the equation. Let's start by expanding the right side of the equation.
- Isolate Constant Terms: Now, we subtract from both sides to isolate the constant terms.
- Combine Like Terms: Simplify the equation by combining like terms.
- Identify Contradiction: We see that , which indicates that there is a contradiction. This means there are no solutions to the equation.