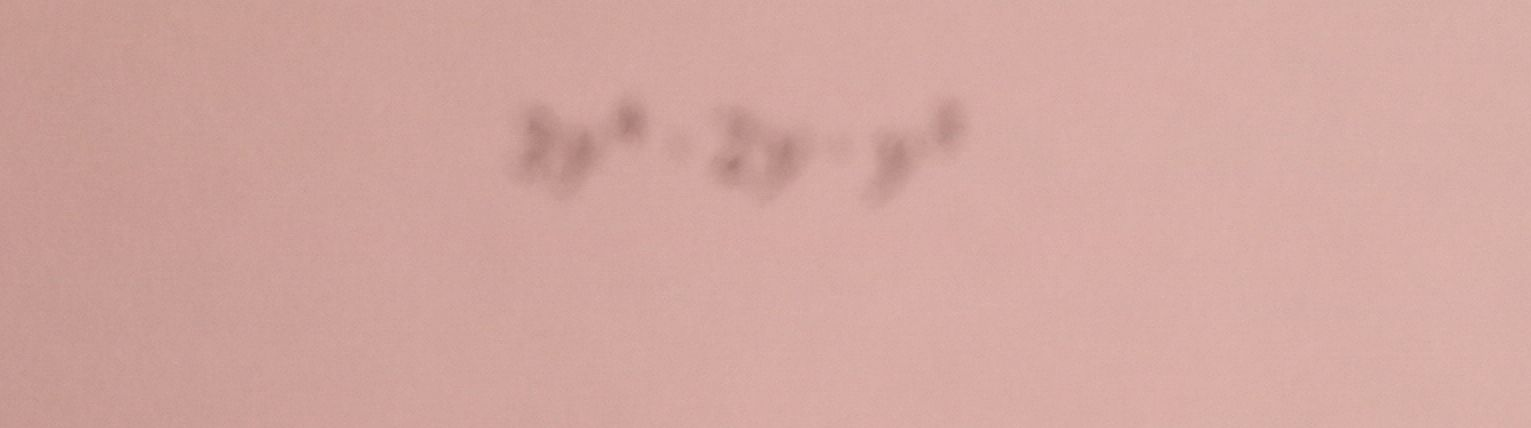AI tutor
Full solution
Q. Simplify =
- Identify Components: Identify the components of the expression.We have the expression , which consists of a constant multiplied by a variable raised to a power, then multiplied by another constant and the variable again, which is also raised to a power.
- Combine Constants: Combine the constants.We can multiply the constants and together.Calculation:
- Apply Exponent Property: Apply the property of exponents to combine the powers of . When multiplying powers with the same base, we add the exponents. Calculation:
- Combine Results: Combine the results from Step and Step .We multiply the constant from Step with the result from Step .Calculation:
More problems from Product property of logarithms
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help