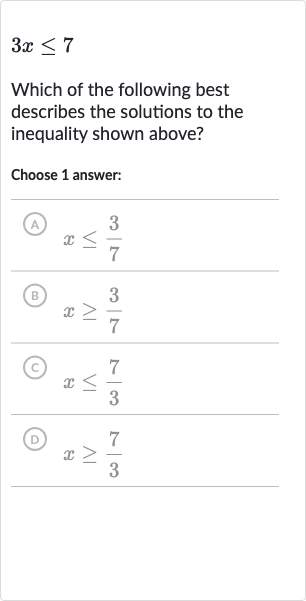
Full solution
Q. Which of the following best describes the solutions to the inequality shown above?Choose answer:(A) (B) (C) (D)
- Solve the inequality: Solve the inequality .To solve for , divide both sides of the inequality by .
- Divide both sides by : Check the solution for any mathematical errors.Dividing both sides of an inequality by a positive number does not change the direction of the inequality. Since is positive, the inequality direction remains the same.
- Check for mathematical errors: Match the solution to the given options.The solution matches option (C) .
More problems from Solve quadratic inequalities
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help