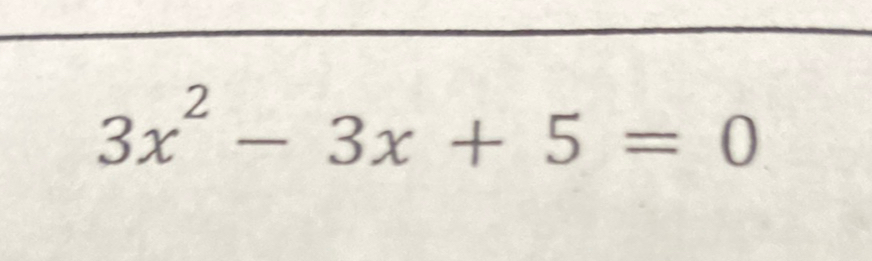3x^(2)-3x+5=0

Question

3x^(2)-3x+5=0

Bytelearn · Accepted Answer

Identify coefficients: Identify the coefficients of the quadratic equation. The quadratic equation is in the form ax^2 + bx + c = 0. For the equation 3x^2 - 3x + 5 = 0, the coefficients are: a = 3, b = -3, and c = 5.Check applicability: Check if the quadratic formula can be applied. The quadratic formula is applicable for all quadratic equations of the form ax^2 + bx + c = 0. Since we have identified the coefficients, we can apply the quadratic formula.Apply quadratic formula: Apply the quadratic formula to find the roots. The quadratic formula is x = (-b ± √(b^2 - 4ac)) / (2a). Let's calculate the discriminant (b^2 - 4ac) first. Discriminant = (-3)^2 - 4(3)(5) Discriminant = 9 - 60 Discriminant = -51Calculate discriminant: Since the discriminant is negative, the roots will be complex numbers. We can now write the roots using the quadratic formula with the discriminant. x = (-(-3) ± √(-51)) / (2 * 3) x = (3 ± √(-51)) / 6Determine complex roots: Simplify the roots by separating the real and imaginary parts. Since √(-51) is an imaginary number, we can write it as √(51)i, where i is the imaginary unit. x = (3 ± √(51)i) / 6Simplify roots: Write the final simplified form of the roots. The roots are: x = (3 + √(51)i) / 6 and x = (3 - √(51)i) / 6

$3 x^{2}-3 x+5=0$

Full solution

More problems from Add, subtract, multiply, and divide polynomials

Related topics

3x2−3x+5=0 3 x^{2}-3 x+5=0 3x2−3x+5=0

$3 x^{2}-3 x+5=0$