Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

What are the critical points for the plane curve defined by the equations x(t)=cot t,y(t)=sin t, and 0 < t < pi ? Write your answer as a list of values of t, separated by commas. For example, if you found t=1 or
t=2, you would enter 1,2 .

What are the critical points for the plane curve defined by the equations $x(t)=\cot t, y(t)=\sin t$ , and \( 0

View step-by-step help

View step-by-step help

Write a linear function: word problems

Full solution

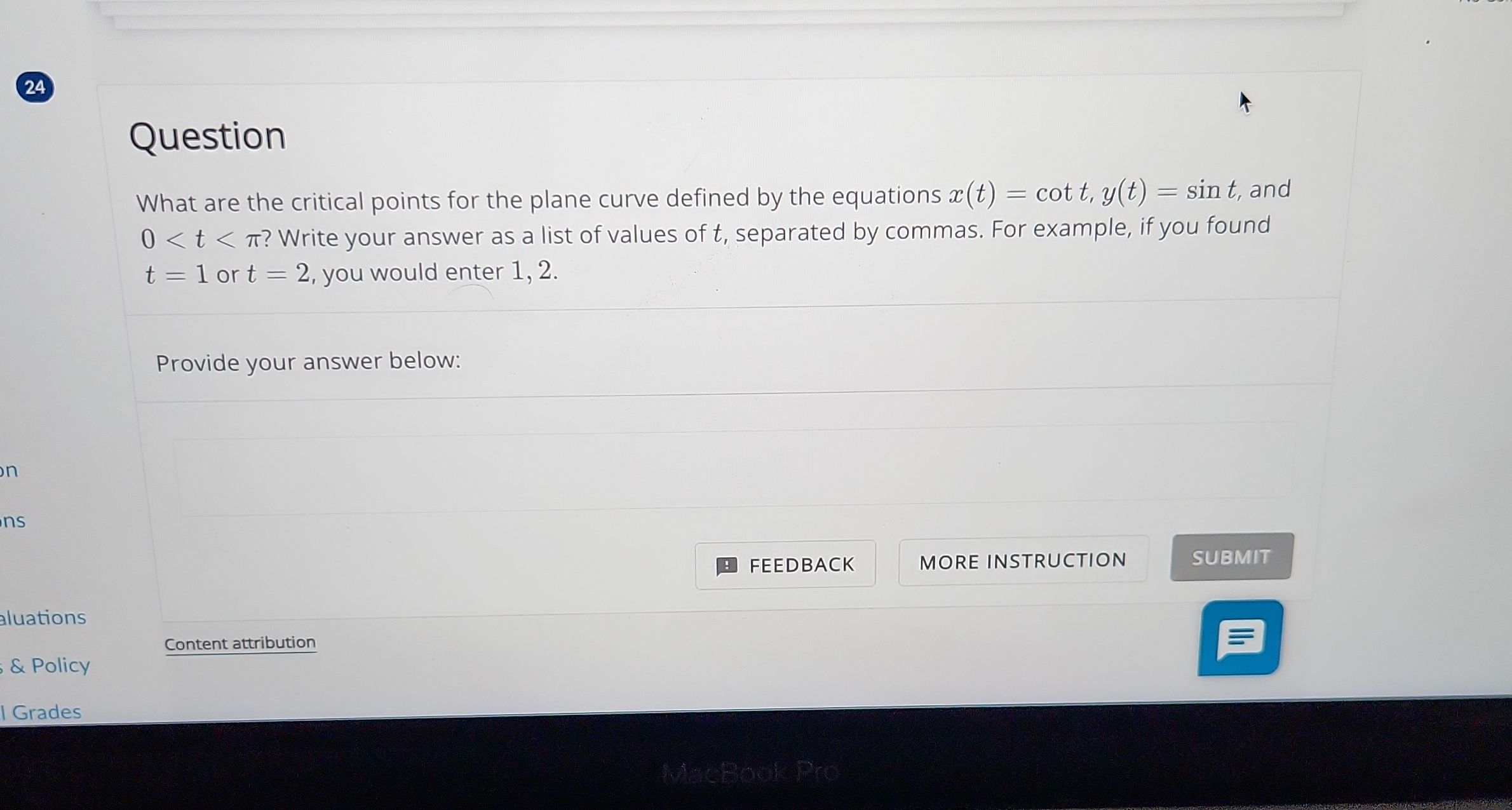
Q. What are the critical points for the plane curve defined by the equations

x(t)=\cot t, y(t)=\sin t

, and

0<t<\pi

? Write your answer as a list of values of

t

, separated by commas. For example, if you found

t=1

or

t=2

, you would enter

1

,

2

.

Question Prompt: Question prompt: What are the critical points for the plane curve defined by the equations $x(t)=\cot t$ , $y(t)=\sin t$ , for 0 < t < \pi?
Derivatives of $x(t)$ and $y(t)$ : Determine the derivatives of $x(t)$ and $y(t)$ with respect to $t$ . The critical points occur where the derivative of $x(t)$ or $y(t)$ is undefined or $0$ .
Derivative of $x(t)$ : Find the derivative of $x(t) = \cot t$ . The derivative of $\cot t$ is $-\csc^2 t$ . $\frac{dx}{dt} = -\csc^2 t$
Derivative of $y(t)$ : Find the derivative of $y(t) = \sin t$ . The derivative of $\sin t$ is $\cos t$ . $\frac{dy}{dt} = \cos t$
Identify Undefined or Zero Values: Identify the values of $t$ where $\frac{dx}{dt}$ and $\frac{dy}{dt}$ are undefined or zero. $\newline$ For $\frac{dx}{dt} = -\csc^2 t$ to be undefined, $\sin t$ must be zero since $\csc t = \frac{1}{\sin t}$ . $\newline$ For $\frac{dy}{dt} = \cos t$ to be zero, $\cos t$ must be zero.
Solve for $\sin t = 0$ : Solve for $t$ where $\sin t = 0$ within the interval $(0, \pi)$ . $\newline$ $\sin t = 0$ at $t = 0$ and $t = \pi$ , but these are not within the open interval $(0, \pi)$ , so they are not considered.
Solve for $\cos t = 0$ : Solve for $t$ where $\cos t = 0$ within the interval $(0, \pi)$ . $\newline$ $\cos t = 0$ at $t = \frac{\pi}{2}$ .
Conclude Critical Points: Conclude the critical points. $\newline$ The only critical point within the interval $(0, \pi)$ is at $t = \frac{\pi}{2}$ .

More problems from Write a linear function: word problems

Question

This equation shows how the time required to screen-print a batch of shirts is related to the number of shirts in the batch.

\newline

t = s + 13

\newline

s

represents the number of shirts in the batch, and the variable

t

represents the time required to screen-print the shirts. How long does it take to screen-print a batch of

4

\newline

_________minutes

Posted 9 months ago

Question

Krysta wants to take piano lessons. She asked a teacher how many new pieces she could expect to learn each month. The teacher gave an estimate of

3

. Write an equation that shows how the total number of pieces Krysta would learn,

y

, depends on the number of months of piano lessons,

x

\newline

y

Posted 9 months ago

Question

Tom bought a boat for

\$3,000

and incurs a daily storage fee of

\$15

. Write a linear function to represent the total amount Tom will owe,

p(x)

x

days to pick it up.

\newline

Posted 9 months ago

Question

180

-page book cover to cover in a single session, at a constant rate. It took him

6

\newline

\newline

y

represent the number of pages left to read after

\newline

t

\newline

Which of the following information about the graph of the relationship is given?

\newline

1

\newline

\newline

x

\newline

\newline

y

\newline

(C) Slope and a point that is not an intercept

\newline

\newline

x

\newline

y

\newline

\newline

y

-intercept and a point that is not an intercept

\newline

(F) Two points that are not intercepts

Posted 10 months ago

Question

A charity organization had to sell

18

tickets to their fundraiser just to cover necessary production costs. They sold each ticket for

\$45

y

represent the net profit (in dollars) when they have sold

x

tickets. Which of the following information about the graph of the relationship is given?

\newline

1

\newline

x

\newline

y

\newline

(C) Slope and a point that is not an intercept

\newline

x

y

\newline

y

-intercept and a point that is not an intercept

\newline

(F) Two points that are not intercepts

Posted 8 months ago

Question

Hiro painted his room. After

3

hours of painting at a rate of

8

square meters per hour, he had

28

square meters left to paint.

\newline

\newline

y

represent the area (in square meters) left to paint after

\newline

x

\newline

Which of the following information about the graph of the relationship is given?

\newline

1

\newline

\newline

x

\newline

\newline

y

\newline

(C) Slope and a point that is not an intercept

\newline

\newline

x

\newline

y

\newline

\newline

y

-intercept and a point that is not an intercept

\newline

(F) Two points that are not intercepts

Posted 8 months ago

Question

Naoya read a book cover to cover in a single session, at a rate of

55

pages per hour. After

4

350

pages left to read.

\newline

y

represent the number of pages left to read after

x

\newline

Complete the equation for the relationship between the number of pages left and number of hours.

\newline

y=

Posted 7 months ago

Question

A teacher purchased

300

colored pencils for an upcoming project. The pencils she ordered come in packs of

20

30

14

packs in all. Write a system of equations to find the number of

20

(x)

30

(y)

the art teacher ordered.

Posted 8 months ago

Question

C=0.25(L-1200)

\newline

C

, in dollars, to the holder of a liability insurance account given a total liability of

L

dollars is given by the equation as long as

C

is positive. By how many dollars does the liability increase when the cost to the holder increases by

1

Posted 8 months ago

Question

P=\frac{2}{5} m+1.5

\newline

P

, in dollars, of a train ticket used to travel a distance of

m

miles is given by the equation. By how many miles does the traveling distance increase if the ticket price increases by

1

Posted 2 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant