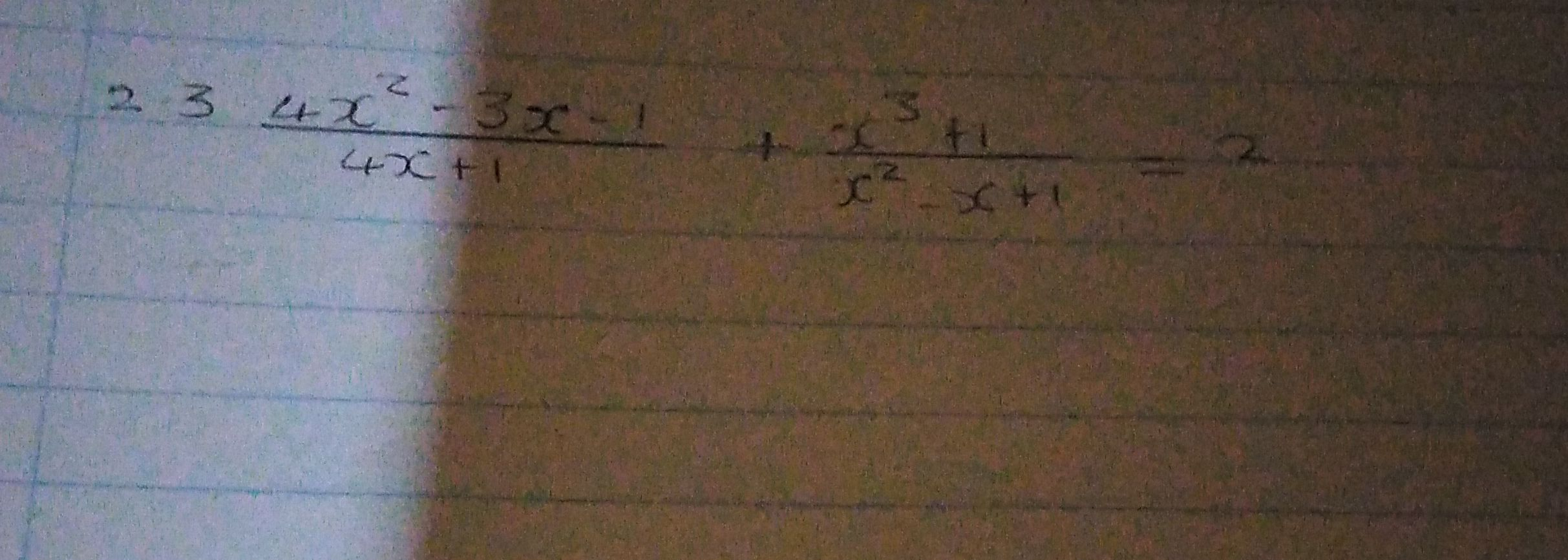(4x^(2)-3x-1)/(4x+1)+(x^(3)+1)/(x^(2)-x+1)=2

Question

Bytelearn · Accepted Answer

Simplify First Term: Simplify the first term 23(4x^(2)-3x-1)/(4x+1). We need to check if the numerator can be factored or if there is a common factor with the denominator. Since there is no obvious common factor and the numerator does not factor nicely with respect to the denominator, we cannot simplify this term further at this point.Simplify Second Term: Simplify the second term (x^(3)+1)/(x^(2)-x+1). We need to check if the numerator can be factored or if there is a common factor with the denominator. The numerator is a sum of cubes, which can be factored as (x+1)(x^(2)-x+1). The denominator is already in its simplest form and does not factor with the numerator. Therefore, this term cannot be simplified further.Combine Terms: Combine the two terms. Since the two terms do not have a common denominator, we cannot combine them into a single fraction. The expression remains as 23(4x^(2)-3x-1)/(4x+1) + (x^(3)+1)/(x^(2)-x+1).Check Expression: Check if the expression equals 2. To check if the expression equals 2, we would need to find a common denominator and combine the terms. However, without specific values for x, we cannot determine if the expression simplifies to 2.

$\frac{4 x^{2}-3 x-1}{4 x+1}+\frac{x^{3}+1}{x^{2}-x+1}=2$

Full solution

More problems from Add, subtract, multiply, and divide polynomials

Related topics

4x2−3x−14x+1+x3+1x2−x+1=2\frac{4 x^{2}-3 x-1}{4 x+1}+\frac{x^{3}+1}{x^{2}-x+1}=2 4x+14x2−3x−1​+x2−x+1x3+1​=2

$\frac{4 x^{2}-3 x-1}{4 x+1}+\frac{x^{3}+1}{x^{2}-x+1}=2$