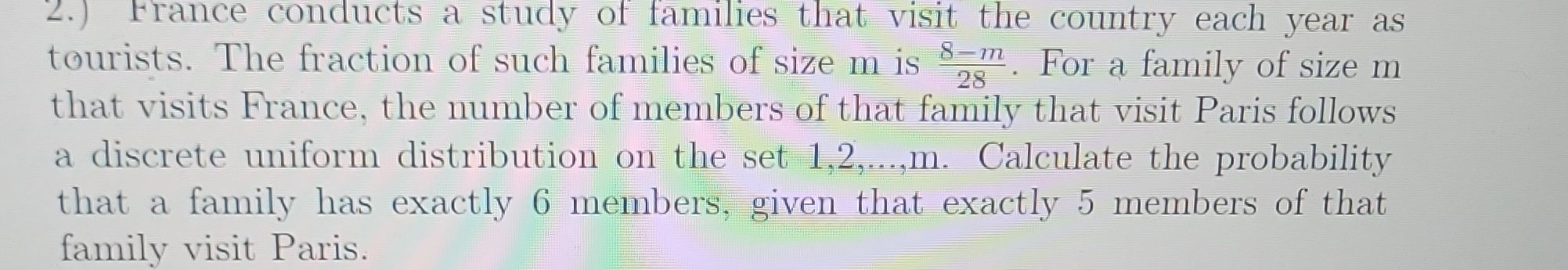
2.) France conducts a study of families that visit the country each year as tourists. The fraction of such families of size m is (8-m)/(28). For a family of size m that visits France, the number of members of that family that visit Paris follows a discrete uniform distribution on the set 1,2,dots,m. Calculate the probability that a family has exactly 6 members, given that exactly 5 members of that family visit Paris.

Question

2.) France conducts a study of families that visit the country each year as tourists. The fraction of such families of size  m is  (8-m)/(28). For a family of size  m that visits France, the number of members of that family that visit Paris follows a discrete uniform distribution on the set  1,2,dots,m. Calculate the probability that a family has exactly 6 members, given that exactly 5 members of that family visit Paris.

Bytelearn · Accepted Answer

Given Fraction of Families: We are given that the fraction of families of size m is (8-m)/28. We want to find the probability that a family has exactly 6 members, given that exactly 5 members visit Paris. This is a conditional probability problem, and we can use the formula P(A|B) = P(A and B) / P(B), where A is the event that a family has exactly 6 members and B is the event that exactly 5 members visit Paris.Calculate P(A): First, we calculate P(A), the probability that a family has exactly 6 members. We substitute m = 6 into the fraction (8-m)/28 to find the probability of a family being of size 6. P(A) = (8-6)/28 = 2/28 = 1/14Calculate P(B): Next, we calculate P(B), the probability that exactly 5 members visit Paris. Since the number of members that visit Paris follows a discrete uniform distribution on the set 1,2,...,m, the probability that any specific number of members visit Paris is 1/m. For a family of size 6, the probability that exactly 5 members visit Paris is 1/6. P(B) = 1/6Calculate P(A and B): Now, we calculate P(A and B), the probability that a family has exactly 6 members and exactly 5 members visit Paris. Since the events are independent (the size of the family does not affect the distribution of who visits Paris), we can multiply the probabilities of A and B. P(A and B) = P(A) * P(B) = (1/14) * (1/6) = 1/84Find P(A|B): Finally, we use the conditional probability formula to find P(A|B), the probability that a family has exactly 6 members given that exactly 5 members visit Paris. P(A|B) = P(A and B) / P(B) = (1/84) / (1/6) = (1/84) * (6/1) = 6/84 = 1/14

Full solution

More problems from One-step inequalities: word problems

Related topics