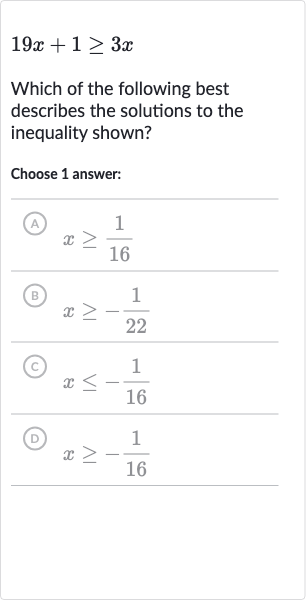
Full solution
Q. Which of the following best describes the solutions to the inequality shown?Choose answer:(A) (B) (C) (D)
- Subtract : To solve the inequality , we need to isolate on one side. We can start by subtracting from both sides of the inequality.Calculation: Simplification:
- Subtract : Next, we subtract from both sides to further isolate the term.Calculation: Simplification:
- Divide by : Now, we divide both sides by to solve for .Calculation: Simplification:
- Final Solution: We have found the solution to the inequality. The solution is , which corresponds to one of the answer choices provided.
More problems from Solve quadratic inequalities
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help