Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

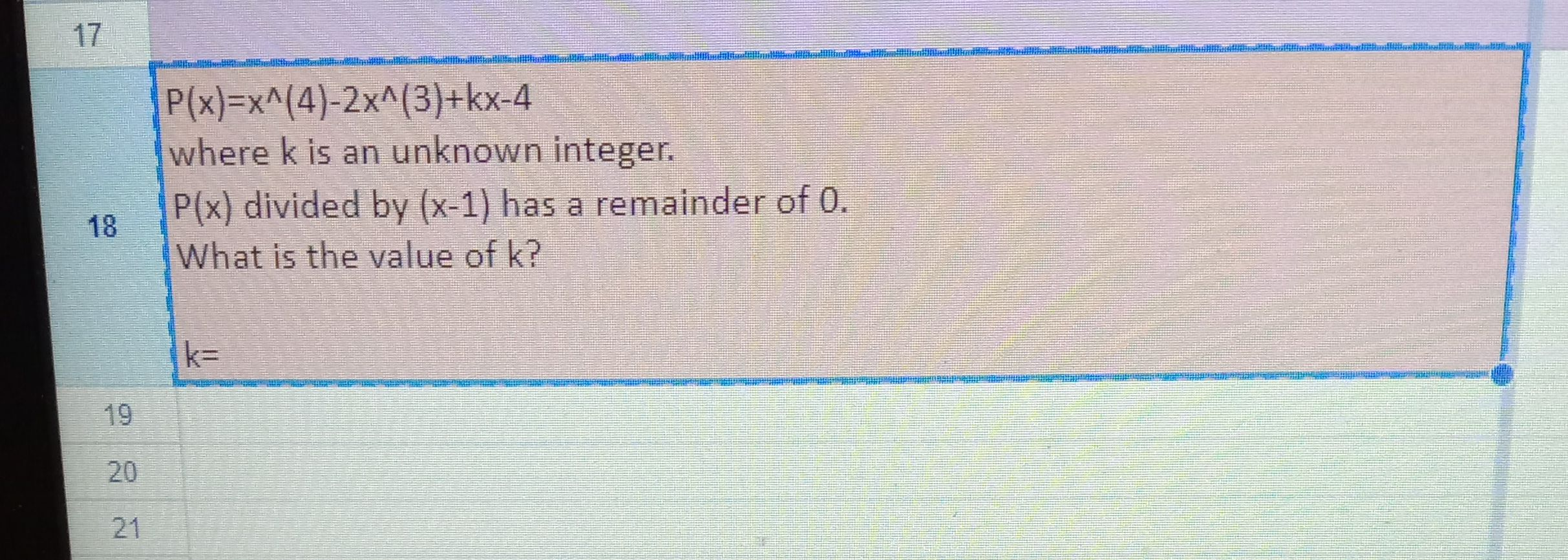
P(x)=x^(4)-2x^(3)+kx-4
where
k is an unknown integer.
P(x) divided by
(x-1) has a remainder of 0 .
What is the value of
k ?

k=

$P(x)=x^4-2 x^3+k x-4$ $\newline$ where $k$ is an unknown integer. $\newline$ $P(x)$ divided by $(x-1)$ has a remainder of $0$ . $\newline$ What is the value of $k$ ? $\newline$ $k=$

View step-by-step help

View step-by-step help

Evaluate piecewise-defined functions

Full solution

Q.

P(x)=x^4-2 x^3+k x-4

\newline

where

k

is an unknown integer.

\newline

P(x)

divided by

(x-1)

has a remainder of

0

.

\newline

What is the value of

k

?

\newline

k=

Apply Remainder Theorem: Apply the Remainder Theorem. $\newline$ The Remainder Theorem states that if a polynomial $P(x)$ is divided by $(x - c)$ and the remainder is $0$ , then $c$ is a root of the polynomial. This means $P(c) = 0$ .
Substitute $x = 1$ : Substitute $x = 1$ into $P(x)$ . $\newline$ Since the remainder is $0$ when $P(x)$ is divided by $(x - 1)$ , we substitute $x = 1$ into the polynomial $P(x)$ to find the value of $k$ . $\newline$ $P(1) = (1)^4 - 2(1)^3 + k(1) - 4$
Simplify the expression: Simplify the expression. $\newline$ $P(1) = 1 - 2 + k - 4$ $\newline$ $P(1) = k - 5$
Set $P(1)$ equal to $0$ : Set $P(1)$ equal to $0$ . Since $P(1)$ must be $0$ for the remainder to be $0$ , we set the simplified expression equal to $0$ . $k - 5 = 0$
Solve for k: Solve for k. $\newline$ Add $5$ to both sides of the equation to solve for k. $\newline$ $k = 5$

More problems from Evaluate piecewise-defined functions

Question

\vec{u}

has an initial point

(4,8)

and a terminal point

(2,4)

\newline

Find the magnitude of

\vec{u}

\newline

Enter an exact answer as an expression with a square root symbol or enter an approximate answer as a decimal rounded to the nearest hundredth.

\newline

\|\vec{u}\|=\square

Posted 3 months ago

Question

\vec{u}

has an initial point

(5,1)

and a terminal point

(-3,4)

\newline

Find the magnitude of

\vec{u}

\newline

Enter an exact answer as an expression with a square root symbol or enter an approximate answer as a decimal rounded to the nearest hundredth.

\newline

\|\vec{u}\|=\square

Posted 3 months ago

Question

Rewrite the expression in the form

x^{n}

\newline

Write the exponent as an integer, fraction, or an exact decimal (not a mixed number).

\newline

\sqrt{x^{\frac{3}{4}} x^{-1}}=\square

Posted 3 months ago

Question

a

. Express your answer as a proper or improper fraction in simplest terms.

\newline

-\frac{5}{6}-\frac{1}{5} a=-\frac{5}{8}

\newline

a=

Posted 2 months ago

Question

Find the value of

x

in the equation below.

\newline

\frac{x}{7}=8

\newline

x=

Posted 2 months ago

Question

Find the value of

x

in the equation below.

\newline

\frac{x}{9}=8

\newline

x=

Posted 2 months ago

Question

Given the function

y=\frac{\sqrt[5]{x^{6}}}{3}

\frac{d y}{d x}

. Express your answer in radical form without using negative exponents, simplifying all fractions.

\newline

\frac{d y}{d x}=

Posted 2 months ago

Question

Given the function

f(x)=\frac{1}{\sqrt[4]{x^{3}}}

f^{\prime}(x)

. Express your answer in radical form without using negative exponents, simplifying all fractions.

\newline

f^{\prime}(x)=

Posted 2 months ago

Question

Solve the following equation for

a

. Be sure to take into account whether a letter is capitalized or not.

\newline

\frac{a}{D}=7

\newline

a=

Posted 2 months ago

Question

Solve the following equation for

A

. Be sure to take into account whether a letter is capitalized or not.

\newline

\frac{A}{g}=m

\newline

A=

Posted 2 months ago