Resources

Testimonials

Plans

Resources

Testimonials

Plans

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

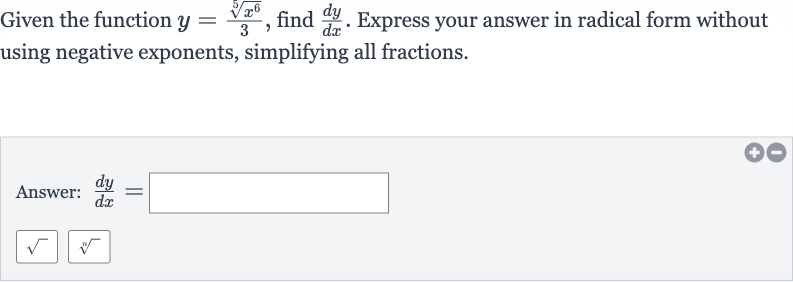
$Given the function y=(root(5)(x^(6)))/(3), find (dy)/(dx). Express your answer in radical form without using negative exponents, simplifying all fractions. Answer: (dy)/(dx)=$

Given the function $y=\frac{\sqrt[5]{x^{6}}}{3}$ , find $\frac{d y}{d x}$ . Express your answer in radical form without using negative exponents, simplifying all fractions. $\newline$ Answer: $\frac{d y}{d x}=$

View step-by-step help

Home

Math Problems

Algebra 1

Evaluate piecewise-defined functions

Full solution

Q. Given the function

y=\frac{\sqrt[5]{x^{6}}}{3}

, find

\frac{d y}{d x}

. Express your answer in radical form without using negative exponents, simplifying all fractions.

\newline

Answer:

\frac{d y}{d x}=

Rewrite function $y$ : To find the derivative of the function $y$ with respect to $x$ , we need to apply the power rule for differentiation. The function $y$ can be rewritten as $y = \frac{x^{\frac{6}{5}}}{3}$ .
Apply power rule: Differentiate the function with respect to $x$ using the power rule, which states that the derivative of $x^n$ with respect to $x$ is $n\cdot x^{n-1}$ . Here, $n$ is $\frac{6}{5}$ . $\frac{dy}{dx} = \frac{6}{5} \cdot \frac{x^{\frac{6}{5} - 1}}{3}$
Simplify derivative exponent: Simplify the exponent in the derivative. The new exponent will be $\frac{6}{5} - \frac{5}{5}$ , which is $\frac{1}{5}$ . $\newline$ $\frac{dy}{dx} = \frac{\frac{6}{5} \cdot x^{\frac{1}{5}}}{3}$
Multiply coefficients: Simplify the fraction by multiplying the coefficients $(\frac{6}{5})$ and $(\frac{1}{3})$ . $\frac{dy}{dx} = \left(\frac{6}{5}\right) \cdot \left(\frac{1}{3}\right) \cdot x^{\frac{1}{5}}$ $\frac{dy}{dx} = \left(\frac{2}{5}\right) \cdot x^{\frac{1}{5}}$
Express in radical form: Express the final answer in radical form without using negative exponents. The fifth root of $x$ can be written as the radical expression $\sqrt[5]{x}$ . $\newline$ $\frac{dy}{dx} = \frac{2}{5} \times \sqrt[5]{x}$