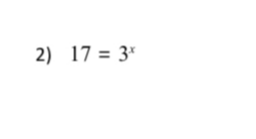AI tutor
Full solution
Q. )
- Recognize Equation Type: Recognize that the equation is an exponential equation.We need to find the value of such that . Since is not a power of , we will likely need to use logarithms to solve for .
- Apply Logarithm: Apply the logarithm to both sides of the equation.Taking the natural logarithm (ln) of both sides gives us .
- Use Power Rule: Use the power rule of logarithms. The power rule of logarithms states that . Applying this rule, we get .
- Solve for x: Solve for x.To isolate , we divide both sides of the equation by . This gives us .
- Calculate x Value: Calculate the value of . Using a calculator, we find that . However, the question prompt asks for the answer as an integer or a fraction in simplest form. Since is not an integer and cannot be expressed as a simple fraction, we leave it in this logarithmic form.