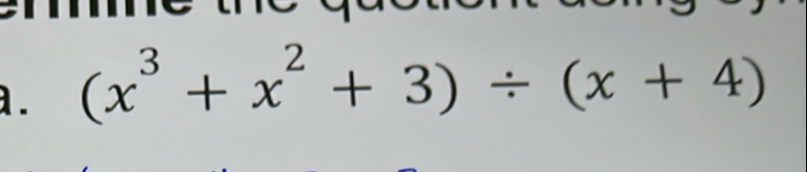AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
Full solution
Q.
- Use polynomial long division: To divide the polynomial by , we will use polynomial long division.
- Divide leading terms: First, we divide the leading term of the numerator, , by the leading term of the denominator, , to get .
- Multiply by result: We then multiply the entire denominator by this result to get .
- Subtract to find remainder: Next, we subtract the product from the original numerator to find the new remainder. This gives us .
- Divide new remainder: Now, we divide the leading term of the new remainder, , by the leading term of the denominator, , to get .
- Multiply by : We multiply the entire denominator by to get .
- Subtract to find next remainder: Subtract this product from the current remainder to find the next remainder. This gives us .
- Divide new remainder: Now, we divide the leading term of the new remainder, , by the leading term of the denominator, , to get .
- Multiply by : We multiply the entire denominator by to get .
- Subtract to find next remainder: Subtract this product from the current remainder to find the next remainder. This gives us .
- Check for completion: Since the degree of the remainder is less than the degree of the denominator , we cannot continue the division process. The result of the division is the quotient plus the remainder over the original divisor.
- Final answer: The quotient we obtained is , and the remainder is . Therefore, the final answer is with a remainder of , which can be written as .
