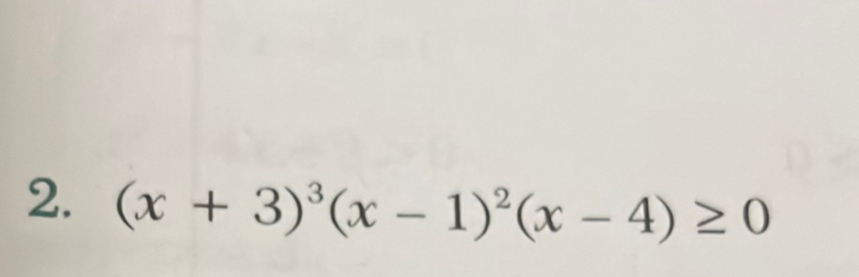Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

(x+3)^(3)(x-1)^(2)(x-4) >= 0

$(x+3)^{3}(x-1)^{2}(x-4) \geq 0$

View step-by-step help

View step-by-step help

Solve quadratic inequalities

Full solution

Q.

(x+3)^{3}(x-1)^{2}(x-4) \geq 0

Identify Zeros: Identify the zeros of the function $(x+3)^3(x-1)^2(x-4)$ . Set each factor to zero: $(x+3) = 0$ gives $x = -3$ . $(x-1) = 0$ gives $x = 1$ . $(x-4) = 0$ gives $x = 4$ . Critical points: $-3$ , $1$ , $4$ .
Determine Intervals: Determine the intervals to test based on the critical points. $\newline$ The critical points divide the number line into four intervals: $(-\infty, -3)$ , $(-3, 1)$ , $(1, 4)$ , $(4, \infty)$ .
Test Sign: Test the sign of $(x+3)^3(x-1)^2(x-4)$ in each interval. $\newline$ For $x < -3$ , choose $x = -4$ : $(-4+3)^3(-4-1)^2(-4-4) = (-1)^3(-5)^2(-8) = -1\cdot25\cdot(-8) = 200$ (positive). $\newline$ For $-3 < x < 1$ , choose $x = 0$ : $(0+3)^3(0-1)^2(0-4) = 3^3(-1)^2(-4) = 27\cdot1\cdot(-4) = -108$ (negative). $\newline$ For $1 < x < 4$ , choose $x = 2$ : $(2+3)^3(2-1)^2(2-4) = 5^3(1)^2(-2) = 125\cdot1\cdot(-2) = -250$ (negative). $\newline$ For $x < -3$ $0$ , choose $x < -3$ $1$ : $x < -3$ $2$ (positive).
Combine Results: Combine the results to form the solution. $\newline$ $(x+3)^3(x-1)^2(x-4) \geq 0$ is satisfied when the expression is positive or zero. $\newline$ The intervals where this occurs are $(-\infty, -3]$ , $[1, 4]$ , and $[4, \infty)$ .

More problems from Solve quadratic inequalities

Question

s

\newline

|s| + 3 \geq 8

\newline

\newline

Write a compound inequality like

1 < x < 3

x < 1

x > 3

. Use integers, proper fractions, or improper fractions in simplest form.

\newline

\newline

Posted 2 months ago

Question

x

\newline

(x - 1)(x + 1) > 0

\newline

\newline

Write a compound inequality like

1 < x < 3

x < 1

x > 3

\newline

Posted 2 months ago

Question

A particular company charges advertisers a one time cost of

\$500

, in addition to

\$4.50

for every one thousand times an advertisement is shown on the company's webpage. An advertiser wants its ad to appear

M

thousand times on the webpage, but does not want to spend more than

\$5,000

. Which of the following inequalities best describes the situation?

\newline

\newline

500+4.50M\geq5,000

\newline

4.50+500M>5,000

\newline

500+4.50M\leq5,000

\newline

500+4.50M<5,000

Posted 2 months ago

Question

7x+1 < x+9

\newline

Which of the following best describes the solutions to the inequality shown?

\newline

1

\newline

x > \frac{4}{3}

\newline

x < \frac{4}{3}

\newline

x < 1

\newline

x < \frac{5}{3}

Posted 4 months ago

Question

52-3x < -14

\newline

Which of the following best describes the solutions to the inequality shown?

\newline

1

\newline

x > -\frac{38}{3}

\newline

x > \frac{38}{3}

\newline

x < 22

\newline

x > 22

Posted 4 months ago

Question

5-3x > 2x+2

\newline

Which of the following best describes the solutions to the inequality shown?

\newline

1

\newline

x < \frac{7}{5}

\newline

x < 3

\newline

x < \frac{3}{5}

\newline

x > \frac{3}{5}

Posted 4 months ago

Question

Rani is a real estate agent. For each house she sells, she pays

\$ 100

in fees, but earns a commission of

1.8 \%

of the selling price of the house. Rani's total profit from a particular house is

\$ 4,580

p

represents the selling price of the house, which equation best models the situation?

\newline

1

\newline

0.018 p-100=4580

\newline

0.018 p+100=4580

\newline

(100-0.018) p=4580

\newline

(100+0.018) p=4580

Posted 2 months ago

Question

A commercial airplane that is

1

500

2

500

-mile journey is traveling at

450

knots in still air when it picks up a tailwind of

150

knots (in the same direction). If

h

is the number of hours remaining in the airplane's flight, which of the following equations best describes the situation?

\newline

1

\mathrm{knot}=1.15

miles per hour (mph)

\newline

1

\newline

1,500+690 h=2,500

\newline

1,500+600 h=2,500

\newline

1,500-600 h=2,500

\newline

1,500-690 h=2,500

Posted 1 month ago

Question

A weeping willow that is

15

feet in height grows to a maximum height of

35

y

years at a constant rate of

24

inches per year. Which of the following equations best describes this situation?

\newline

1

=12

\newline

1

\newline

35=15+2 y

\newline

35=15+24 y

\newline

35=15-2 y

\newline

35=15-24 y

Posted 4 months ago

Question

The gas mileage for a car is

23

miles per gallon when the car travels at

60

miles per hour. The car begins a trip with

13

gallons in its tank, travels at an average speed of

60

miles per hour for

h

hours, and ends the trip with

10

gallons in its tank. Which of the following equations best models this situation?

\newline

1

\newline

13-\frac{23 h}{60}=10

\newline

13-\frac{60 h}{23}=10

\newline

\frac{13-60 h}{23}=10

\newline

\frac{13-23 h}{60}=10

Posted 3 months ago