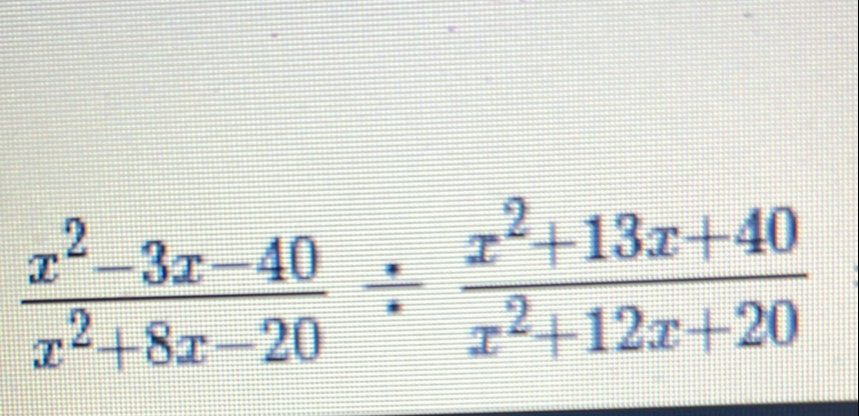(x^(2)-3x-40)/(x^(2)+8x-20)÷(x^(2)+13 x+40)/(x^(2)+12 x+20)

Question

Bytelearn · Accepted Answer

Factor Numerators: First, we need to factor the numerators and denominators of both fractions if possible. Let's start with the numerator of the first fraction: $x^2-3x-40$. We look for two numbers that multiply to -40 and add to -3. These numbers are -8 and 5. So, $x^2-3x-40$ factors to $(x-8)(x+5)$.Factor Denominators: Now, let's factor the denominator of the first fraction: $x^2+8x-20$. We look for two numbers that multiply to -20 and add to 8. These numbers are 10 and -2. So, $x^2+8x-20$ factors to $(x+10)(x-2)$.Factor Second Fraction: Next, we factor the numerator of the second fraction: $x^2+13x+40$. We look for two numbers that multiply to 40 and add to 13. These numbers are 8 and 5. So, $x^2+13x+40$ factors to $(x+8)(x+5)$.Factor Second Denominator: Finally, we factor the denominator of the second fraction: $x^2+12x+20$. We look for two numbers that multiply to 20 and add to 12. These numbers are 10 and 2. So, $x^2+12x+20$ factors to $(x+10)(x+2)$.Rewrite Original Expression: Now we rewrite the original expression with the factored forms: $$\frac{(x-8)(x+5)}{(x+10)(x-2)} ÷ \frac{(x+8)(x+5)}{(x+10)(x+2)}$$Reciprocal and Multiply: Recall that dividing by a fraction is the same as multiplying by its reciprocal. So we take the reciprocal of the second fraction and multiply: $$\frac{(x-8)(x+5)}{(x+10)(x-2)} \times \frac{(x+10)(x+2)}{(x+8)(x+5)}$$Cancel Common Factors: Next, we cancel out the common factors in the numerator and the denominator: The $(x+5)$ terms cancel out, as do the $(x+10)$ terms. We are left with: $$\frac{(x-8)}{(x-2)} \times \frac{(x+2)}{(x+8)}$$Multiply Remaining Factors: Now we multiply the remaining factors across the numerator and the denominator: $$\frac{(x-8)(x+2)}{(x-2)(x+8)}$$Expand Numerator and Denominator: We can expand the numerator and the denominator to check if further simplification is possible: Numerator: $(x-8)(x+2) = x^2 - 8x + 2x - 16 = x^2 - 6x - 16$ Denominator: $(x-2)(x+8) = x^2 + 8x - 2x - 16 = x^2 + 6x - 16$Final Simplified Form: We see that the numerator and the denominator are not the same and cannot be simplified further. Therefore, the final simplified form of the expression is: $$\frac{x^2 - 6x - 16}{x^2 + 6x - 16}$$

$\frac{x^{2}-3 x-40}{x^{2}+8 x-20} \div \frac{x^{2}+13 x+40}{x^{2}+12 x+20}$

Full solution

More problems from Divide polynomials using long division

Related topics

x2−3x−40x2+8x−20÷x2+13x+40x2+12x+20 \frac{x^{2}-3 x-40}{x^{2}+8 x-20} \div \frac{x^{2}+13 x+40}{x^{2}+12 x+20} x2+8x−20x2−3x−40​÷x2+12x+20x2+13x+40​

$\frac{x^{2}-3 x-40}{x^{2}+8 x-20} \div \frac{x^{2}+13 x+40}{x^{2}+12 x+20}$