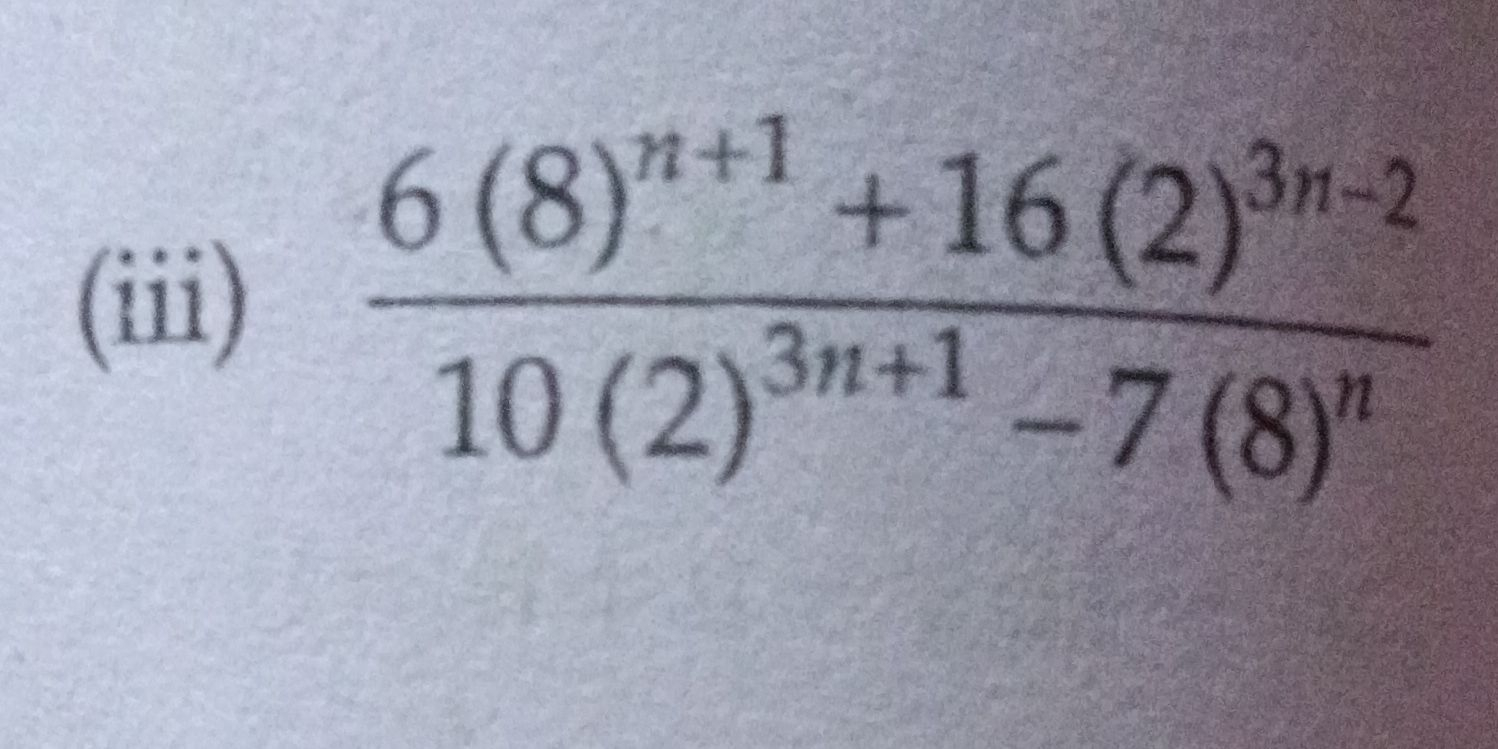Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

(iii) (6(8)^(n+1)+16(2)^(3n-2))/(10(2)^(3n+1)-7(8)^(n))

(iii) 6(8)n+1+16(2)3n−210(2)3n+1−7(8)n \frac{6(8)^{n+1}+16(2)^{3 n-2}}{10(2)^{3 n+1}-7(8)^{n}}

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Add, subtract, multiply, and divide polynomialsright chevron icon

Full solution

Q. (iii) 6(8)n+1+16(2)3n−210(2)3n+1−7(8)n \frac{6(8)^{n+1}+16(2)^{3 n-2}}{10(2)^{3 n+1}-7(8)^{n}}
  1. Simplify terms involving powers: First, simplify the terms involving powers of 88 and 22.
    (6(8)(n+1)=6×8×8n=48×8n,(6(8)^{(n+1)} = 6 \times 8 \times 8^n = 48 \times 8^n,
    16(2)(3n−2)=16×2(3n−2),16(2)^{(3n-2)} = 16 \times 2^{(3n-2)},
    10(2)(3n+1)=10×2×2(3n)=20×2(3n),10(2)^{(3n+1)} = 10 \times 2 \times 2^{(3n)} = 20 \times 2^{(3n)},
    7(8)(n)=7×8n.7(8)^{(n)} = 7 \times 8^n.
  2. Rewrite using simplified terms: Rewrite the expression using simplified terms: (48⋅8n+16⋅23n−2)/(20⋅23n−7⋅8n)(48 \cdot 8^n + 16 \cdot 2^{3n-2}) / (20 \cdot 2^{3n} - 7 \cdot 8^n).
  3. Recognize and substitute: Recognize that 8n=(23)n=23n8^n = (2^3)^n = 2^{3n} and substitute:\newline(48⋅23n+16⋅23n−2)/(20⋅23n−7⋅23n)(48 \cdot 2^{3n} + 16 \cdot 2^{3n-2}) / (20 \cdot 2^{3n} - 7 \cdot 2^{3n}).
  4. Factor out common terms: Factor out common terms in the numerator and denominator:\newline23n−2×(48×4+16)/23n×(20−7)2^{3n-2} \times (48 \times 4 + 16) / 2^{3n} \times (20 - 7),\newline=23n−2×(192+16)/23n×13= 2^{3n-2} \times (192 + 16) / 2^{3n} \times 13,\newline=23n−2×208/23n×13= 2^{3n-2} \times 208 / 2^{3n} \times 13.
  5. Reduce powers of 22: Simplify by reducing the powers of 22:\newline23n−2/23n=2−22^{3n-2} / 2^{3n} = 2^{-2},\newline=2−2×208/13= 2^{-2} \times 208 / 13,\newline=208/(13×4)= 208 / (13 \times 4),\newline=208/52= 208 / 52.
  6. Perform division: Perform the division: 208/52=4208 / 52 = 4.

More problems from Add, subtract, multiply, and divide polynomials

Question
Find the degree of this polynomial.\newline`5b^{10} + 3b^3`\newline_______
Get tutor helpright-arrow

Posted 2 months ago

Question
Subtract.\newline(9a+5)−(2a+4)(9a + 5) - (2a + 4)\newline____
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the product. Simplify your answer. \newline−3v2(v2−9)-3v^2(v^2 - 9)\newline________
Get tutor helpright-arrow

Posted 1 month ago

Question
Find the product. Simplify your answer.\newline(v−3)(4v+1)(v - 3)(4v + 1)\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the square. Simplify your answer.\newline(3y+2)2(3y + 2)^2\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Divide. If there is a remainder, include it as a simplified fraction.\newline(24t2+36t)÷6t(24t^2 + 36t) \div 6t\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Is the function q(x)=x6−9 q(x) = x^6 - 9 even, odd, or neither?\newlineChoices:\newline[[even][odd][neither]]\text{[[even][odd][neither]]}
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the product. Simplify your answer. \newline−3q2(−3q2+q)-3q^2(-3q^2 + q)\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the product. Simplify your answer.\newline(r+3)(4r+2)(r + 3)(4r + 2)\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the roots of the factored polynomial.\newline(x+7)(x+4)(x + 7)(x + 4)\newlineWrite your answer as a list of values separated by commas.\newlinex=x = ____
Get tutor helpright-arrow

Posted 2 months ago

View all (427)