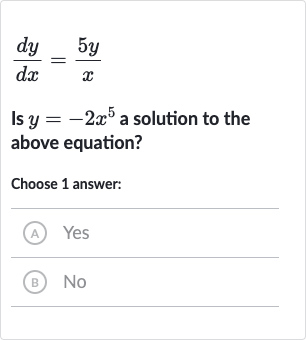
Full solution
Q. Is a solution to the above equation?Choose answer:(A) Yes(B)
- Differentiate : To determine if is a solution to the differential equation , we need to differentiate with respect to and then substitute the result into the differential equation to see if it holds true.Let's differentiate with respect to .
- Substitute into equation: Now we substitute into the right side of the differential equation to see if it equals the derivative we found.
- Compare derivative and equation: We compare the derivative with the expression we found by substituting into the differential equation, which is also . Since both sides are equal, is indeed a solution to the differential equation .
More problems from Is (x, y) a solution to the nonlinear equation?
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help