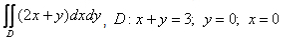Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

∬_(D)(2x+y)dxdy,D:x+y=3;y=0;x=0

$\iint_{D}(2 x+y) d x d y, D: x+y=3 ; y=0 ; x=0$

View step-by-step help

View step-by-step help

Find limits involving trigonometric functions

Full solution

Q.

\iint_{D}(2 x+y) d x d y, D: x+y=3 ; y=0 ; x=0

Determine region D: Determine the region D for integration. $\newline$ The region D is bounded by the lines $x+y=3$ , $y=0$ , and $x=0$ . This forms a right triangle in the first quadrant with vertices at $(0,0)$ , $(3,0)$ , and $(0,3)$ .
Set up double integral: Set up the double integral. Since $y$ ranges from $0$ to $3$ (from the line $y=0$ to the line $x+y=3$ where $x=0$ ), and $x$ ranges from $0$ to $3-y$ (from $x=0$ to $x+y=3$ ), the integral is set up as: $0$ $1$ .
Integrate with respect to x: Integrate with respect to x. $\int_{x=0}^{3-y} (2x+y) \, dx = [x^2 + yx]_{x=0}^{3-y}$ = $[(3-y)^2 + y(3-y)] - [0 + 0]$ = $(3-y)^2 + 3y - y^2$ .
Simplify expression: Simplify the expression. $\newline$ $(3-y)^2 + 3y - y^2 = 9 - 6y + y^2 + 3y - y^2$ $\newline$ $= 9 - 3y.$

More problems from Find limits involving trigonometric functions

Question

\lim _{x \rightarrow \infty} \frac{x+1}{x^{2}+1}

\newline

1

\newline

1

\newline

2

\newline

0

\newline

(D) The limit is unbounded

Posted 3 months ago

Question

Solve the differential equation.

\newline

\frac{dy}{dx}=e^{2x-2y}

Posted 2 months ago

Question

Find the derivative of each function using the limit definition.

\newline

\newline

f(x)=x^{2}+3x-5

Posted 2 months ago

Question

Click and drag like terms onto each other to simplify fully.

\newline

2+4 x+1+4

\newline

You must answer all questions above in order to submit.

Posted 2 months ago

Question

Click and drag like terms onto each other to simplify fully.

\newline

1-x+x+2 x+3

\newline

You must answer all questions above in order to submit.

Posted 2 months ago

Question

y

makes the equation below true?

\newline

9 y-2=25

\newline

2

\newline

3

\newline

5

\newline

9

Posted 2 months ago

Question

z

makes the equation below true?

\newline

10 z+5=75

\newline

7

\newline

10

\newline

11

\newline

15

Posted 2 months ago

Question

y

makes the equation below true?

\newline

2 y+5=21

\newline

5

\newline

8

\newline

14

\newline

16

Posted 2 months ago

Question

y

makes the equation below true?

\newline

4 y-5=23

\newline

6

\newline

7

\newline

14

\newline

23

Posted 2 months ago

Question

y

makes the equation below true?

\newline

6 y-1=17

\newline

3

\newline

6

\newline

15

\newline

16

Posted 2 months ago