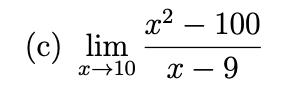Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Evaluate
lim_(x rarr10)(x^(2)-100)/(x-9)

Evaluate $\lim_{x \to 10}\frac{x^{2}-100}{x-9}$

View step-by-step help

View step-by-step help

Quadratic equation with complex roots

Full solution

Q. Evaluate

\lim_{x \to 10}\frac{x^{2}-100}{x-9}

Identify Limit Form: Identify the form of the limit. $\newline$ We need to determine the form of the limit as $x$ approaches $10$ for the function $\frac{x^2 - 100}{x - 9}$ . $\newline$ Substitute $x = 10$ into the function to see if the limit can be directly calculated. $\newline$ $\frac{10^2 - 100}{10 - 9} = \frac{100 - 100}{10 - 9} = \frac{0}{1}$ $\newline$ Since we get $\frac{0}{1}$ , which is defined, we can conclude that the limit exists and is equal to $0$ .
Substitute $x = 10$ : Realize that there is a mistake in the previous step. $\newline$ We need to re-evaluate the form of the limit because the function $(x^2 - 100)/(x - 9)$ simplifies to a different form when $x$ approaches $10$ . $\newline$ Let's factor the numerator and see if we can simplify the expression. $\newline$ $x^2 - 100$ can be factored as $(x + 10)(x - 10)$ . $\newline$ Now the function becomes $((x + 10)(x - 10))/(x - 9)$ .

More problems from Quadratic equation with complex roots

Question

\newline

8i + 6i

\newline

\newline

Write your answer in the form

a + bi

\newline

\underline{\hspace{1cm}}

\newline

Posted 2 months ago

Question

Find the complex conjugate of the given number.

\newline

4 + 10i

\newline

\newline

Write your answer in the form

a + bi

\newline

Posted 1 month ago

Question

\newline

\frac{{-4i}}{{-9i}}

\newline

\newline

Write your answer in the form

a + bi

. Reduce all fractions.

\newline

\_\_\_\_\_

\newline

Posted 1 month ago

Question

Combine the like terms to create an equivalent expression.

\newline

7k-k+19=\boxed{\phantom{0}}

Posted 4 months ago

Question

Apply the distributive property to factor out the greatest common factor.

\newline

9+12 n=

Posted 1 month ago

Question

Solve the equation.

\newline

\begin{aligned} & 12=n-9 \\ n= & \square \end{aligned}

Posted 4 months ago

Question

What is the amplitude of

y=-\sin (8 x-3)+5

\newline

Posted 2 months ago

Question

What is the period of

\newline

y=4 \sin (-2 x+7)-1 \text { ? }

\newline

Give an exact value.

\newline

Posted 1 month ago

Question

3 \cdot(3+20 i)=

\newline

Your answer should be a complex number in the form

a+b i

a

b

are real numbers.

Posted 3 months ago

Question

(35-23 i)+(13+25 i)=

\newline

Express your answer in the form

(a+b i)

Posted 1 month ago