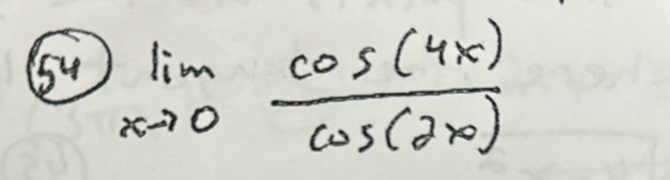AI tutor
Full solution
Q. ()
- Given Limit Expression: We are given the limit expression: To solve this limit, we will directly substitute the value of as , since and are continuous functions and there is no indeterminate form.
- Substitute : Substitute into the expression:
- Simplify Using : Simplify the expression using the fact that :
- Final Simplification: Since , the expression simplifies to:
- Simplify Fraction: Simplify the fraction:
More problems from Evaluate expression when two complex numbers are given
QuestionGet tutor help
QuestionGet tutor help