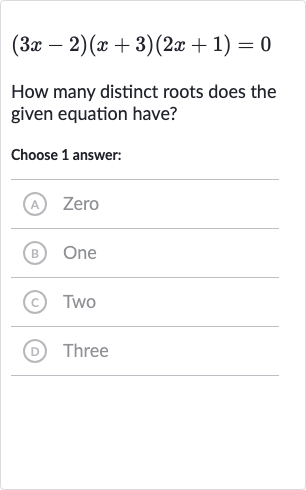
(3x-2)(x+3)(2x+1)=0 How many distinct roots does the given equation have? Choose 1 answer: (A) Zero (B) One (c) Two (D) Three

Question

Bytelearn · Accepted Answer

Equation factors: The given equation is a product of three factors set equal to zero: (3x-2)(x+3)(2x+1)=0. To find the roots, we need to set each factor equal to zero and solve for x.Solving first factor: First factor: 3x - 2 = 0 To solve for x, we add 2 to both sides of the equation: 3x - 2 + 2 = 0 + 2 3x = 2 Now, we divide both sides by 3 to isolate x: 3x/3 = 2/3 x = 2/3 We have found the first root, x = 2/3.Solving second factor: Second factor: x + 3 = 0 To solve for x, we subtract 3 from both sides of the equation: x + 3 - 3 = 0 - 3 x = -3 We have found the second root, x = -3.Solving third factor: Third factor: 2x + 1 = 0 To solve for x, we subtract 1 from both sides of the equation: 2x + 1 - 1 = 0 - 1 2x = -1 Now, we divide both sides by 2 to isolate x: 2x/2 = -1/2 x = -1/2 We have found the third root, x = -1/2.Number of distinct roots: We have found three distinct roots for the equation: x = 2/3, x = -3, and x = -1/2. Therefore, the correct answer to the question of how many distinct roots the equation has is three.

$(3 x-2)(x+3)(2 x+1)=0$ $\newline$ How many distinct roots does the given equation have? $\newline$ Choose $1$ answer: $\newline$ (A) Zero $\newline$ (B) One $\newline$ (c) Two $\newline$ (D) Three

Full solution

More problems from Find the roots of factored polynomials

Related topics

(3x−2)(x+3)(2x+1)=0 (3 x-2)(x+3)(2 x+1)=0 (3x−2)(x+3)(2x+1)=0\newlineHow many distinct roots does the given equation have?\newlineChoose 111 answer:\newline(A) Zero\newline(B) One\newline(c) Two\newline(D) Three

$(3 x-2)(x+3)(2 x+1)=0$ $\newline$ How many distinct roots does the given equation have? $\newline$ Choose $1$ answer: $\newline$ (A) Zero $\newline$ (B) One $\newline$ (c) Two $\newline$ (D) Three