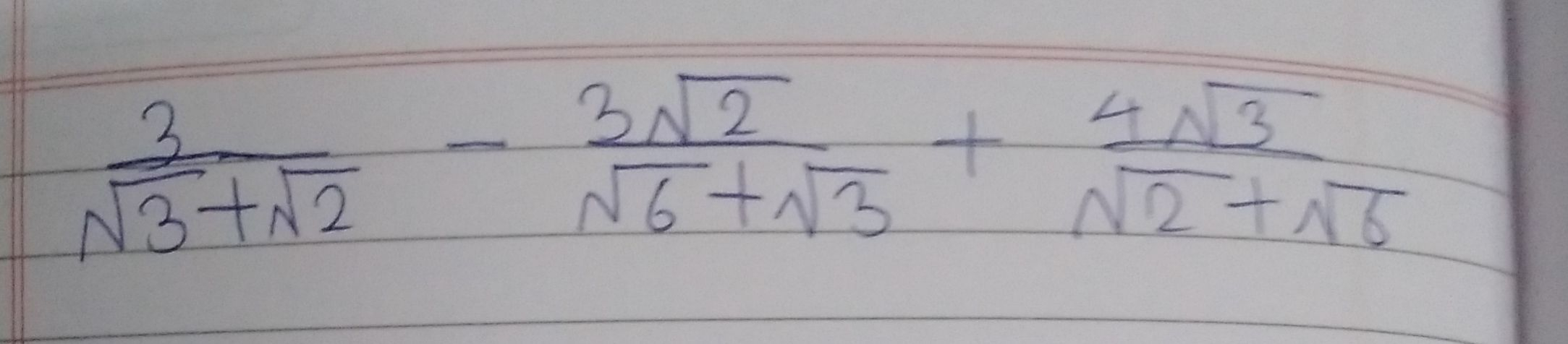Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

(3)/(sqrt3+sqrt2)-(3sqrt2)/(sqrt6+sqrt3)+(4sqrt3)/(sqrt2+sqrt6)

33+2−326+3+432+6 \frac{3}{\sqrt{3}+\sqrt{2}}-\frac{3 \sqrt{2}}{\sqrt{6}+\sqrt{3}}+\frac{4 \sqrt{3}}{\sqrt{2}+\sqrt{6}}

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Add, subtract, multiply, and divide polynomialsright chevron icon

Full solution

Q. 33+2−326+3+432+6 \frac{3}{\sqrt{3}+\sqrt{2}}-\frac{3 \sqrt{2}}{\sqrt{6}+\sqrt{3}}+\frac{4 \sqrt{3}}{\sqrt{2}+\sqrt{6}}
  1. Rationalize First Fraction: To simplify the expression, we will rationalize the denominators of each fraction. Rationalize the denominator of the first fraction: (33+2)(\frac{3}{\sqrt{3}+\sqrt{2}}). Multiply the numerator and denominator by the conjugate of the denominator: (3−2)(\sqrt{3}-\sqrt{2}). (33+2)∗(3−2)(3−2)(\frac{3}{\sqrt{3}+\sqrt{2}}) * \frac{(\sqrt{3}-\sqrt{2})}{(\sqrt{3}-\sqrt{2})}
  2. Simplify First Fraction: Perform the multiplication in the numerator and denominator.\newlineNumerator: 3(3−2)=33−323(\sqrt{3}-\sqrt{2}) = 3\sqrt{3} - 3\sqrt{2}\newlineDenominator: (3+2)(3−2)=32−22=3−2=1(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2}) = \sqrt{3}^2 - \sqrt{2}^2 = 3 - 2 = 1\newlineSo, 33+2=33−32\frac{3}{\sqrt{3}+\sqrt{2}} = 3\sqrt{3} - 3\sqrt{2}
  3. Rationalize Second Fraction: Rationalize the denominator of the second fraction: (32)/(6+3)(3\sqrt{2})/(\sqrt{6}+\sqrt{3}). Multiply the numerator and denominator by the conjugate of the denominator: (6−3)(\sqrt{6}-\sqrt{3}). (32)/(6+3)×(6−3)/(6−3)(3\sqrt{2})/(\sqrt{6}+\sqrt{3}) \times (\sqrt{6}-\sqrt{3})/(\sqrt{6}-\sqrt{3})
  4. Simplify Second Fraction: Perform the multiplication in the numerator and denominator.\newlineNumerator: 32(6−3)=312−363\sqrt{2}(\sqrt{6}-\sqrt{3}) = 3\sqrt{12} - 3\sqrt{6}\newlineDenominator: (6+3)(6−3)=62−32=6−3=3(\sqrt{6}+\sqrt{3})(\sqrt{6}-\sqrt{3}) = \sqrt{6}^2 - \sqrt{3}^2 = 6 - 3 = 3\newlineSo, 326+3=312−363\frac{3\sqrt{2}}{\sqrt{6}+\sqrt{3}} = \frac{3\sqrt{12} - 3\sqrt{6}}{3}
  5. Simplify Second Fraction: Simplify the numerator of the second fraction. \newline3123\sqrt{12} can be simplified to 3(4⋅3)=3⋅23=633\sqrt{(4\cdot3)} = 3\cdot2\sqrt{3} = 6\sqrt{3}\newlineSo, (312−36)/3=(63−36)/3(3\sqrt{12} - 3\sqrt{6})/3 = (6\sqrt{3} - 3\sqrt{6})/3
  6. Rationalize Third Fraction: Divide each term in the numerator by the denominator.\newline(63−36)/3=23−6(6\sqrt{3} - 3\sqrt{6})/3 = 2\sqrt{3} - \sqrt{6}\newlineSo, (32)/(6+3)=23−6(3\sqrt{2})/(\sqrt{6}+\sqrt{3}) = 2\sqrt{3} - \sqrt{6}
  7. Simplify Third Fraction: Rationalize the denominator of the third fraction: (43)/(2+6)(4\sqrt{3})/(\sqrt{2}+\sqrt{6}). Multiply the numerator and denominator by the conjugate of the denominator: (2−6)(\sqrt{2}-\sqrt{6}). (43)/(2+6)×(2−6)/(2−6)(4\sqrt{3})/(\sqrt{2}+\sqrt{6}) \times (\sqrt{2}-\sqrt{6})/(\sqrt{2}-\sqrt{6})
  8. Simplify Third Fraction: Perform the multiplication in the numerator and denominator.\newlineNumerator: 43(2−6)=46−4184\sqrt{3}(\sqrt{2}-\sqrt{6}) = 4\sqrt{6} - 4\sqrt{18}\newlineDenominator: (2+6)(2−6)=22−62=2−6=−4(\sqrt{2}+\sqrt{6})(\sqrt{2}-\sqrt{6}) = \sqrt{2}^2 - \sqrt{6}^2 = 2 - 6 = -4\newlineSo, 432+6=46−418−4\frac{4\sqrt{3}}{\sqrt{2}+\sqrt{6}} = \frac{4\sqrt{6} - 4\sqrt{18}}{-4}
  9. Combine Fractions: Simplify the numerator of the third fraction.\newline4184\sqrt{18} can be simplified to 49⋅2=4⋅32=1224\sqrt{9\cdot2} = 4\cdot3\sqrt{2} = 12\sqrt{2}\newlineSo, (46−418)/(−4)=(46−122)/(−4)(4\sqrt{6} - 4\sqrt{18})/(-4) = (4\sqrt{6} - 12\sqrt{2})/(-4)
  10. Combine Like Terms: Divide each term in the numerator by the denominator.\newline(46−122)/(−4)=−6+32(4\sqrt{6} - 12\sqrt{2})/(-4) = -\sqrt{6} + 3\sqrt{2}\newlineSo, (43)/(2+6)=−6+32(4\sqrt{3})/(\sqrt{2}+\sqrt{6}) = -\sqrt{6} + 3\sqrt{2}
  11. Combine Like Terms: Divide each term in the numerator by the denominator.\newline(46−122)/(−4)=−6+32(4\sqrt{6} - 12\sqrt{2})/(-4) = -\sqrt{6} + 3\sqrt{2}\newlineSo, (43)/(2+6)=−6+32(4\sqrt{3})/(\sqrt{2}+\sqrt{6}) = -\sqrt{6} + 3\sqrt{2}Combine all the simplified fractions.\newline(33−32)−(23−6)+(−6+32)(3\sqrt{3} - 3\sqrt{2}) - (2\sqrt{3} - \sqrt{6}) + (-\sqrt{6} + 3\sqrt{2})
  12. Combine Like Terms: Divide each term in the numerator by the denominator.\newline(46−122)/(−4)=−6+32(4\sqrt{6} - 12\sqrt{2})/(-4) = -\sqrt{6} + 3\sqrt{2}\newlineSo, (43)/(2+6)=−6+32(4\sqrt{3})/(\sqrt{2}+\sqrt{6}) = -\sqrt{6} + 3\sqrt{2}Combine all the simplified fractions.\newline(33−32)−(23−6)+(−6+32)(3\sqrt{3} - 3\sqrt{2}) - (2\sqrt{3} - \sqrt{6}) + (-\sqrt{6} + 3\sqrt{2})Combine like terms.\newline33−32−23+6−6+323\sqrt{3} - 3\sqrt{2} - 2\sqrt{3} + \sqrt{6} - \sqrt{6} + 3\sqrt{2}\newline=(33−23)+(−32+32)+(6−6)= (3\sqrt{3} - 2\sqrt{3}) + (-3\sqrt{2} + 3\sqrt{2}) + (\sqrt{6} - \sqrt{6})\newline=3+0+0= \sqrt{3} + 0 + 0\newline=3= \sqrt{3}

More problems from Add, subtract, multiply, and divide polynomials

Question
Find the degree of this polynomial.\newline`5b^{10} + 3b^3`\newline_______
Get tutor helpright-arrow

Posted 5 months ago

Question
Subtract.\newline(9a+5)−(2a+4)(9a + 5) - (2a + 4)\newline____
Get tutor helpright-arrow

Posted 5 months ago

Question
Find the product. Simplify your answer. \newline−3v2(v2−9)-3v^2(v^2 - 9)\newline________
Get tutor helpright-arrow

Posted 5 months ago

Question
Find the product. Simplify your answer.\newline(v−3)(4v+1)(v - 3)(4v + 1)\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Find the square. Simplify your answer.\newline(3y+2)2(3y + 2)^2\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Divide. If there is a remainder, include it as a simplified fraction.\newline(24t2+36t)÷6t(24t^2 + 36t) \div 6t\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Is the function q(x)=x6−9 q(x) = x^6 - 9 even, odd, or neither?\newlineChoices:\newline[[even][odd][neither]]\text{[[even][odd][neither]]}
Get tutor helpright-arrow

Posted 9 months ago

Question
Find the product. Simplify your answer. \newline−3q2(−3q2+q)-3q^2(-3q^2 + q)\newline______
Get tutor helpright-arrow

Posted 9 months ago

Question
Find the product. Simplify your answer.\newline(r+3)(4r+2)(r + 3)(4r + 2)\newline______
Get tutor helpright-arrow

Posted 9 months ago

Question
Find the roots of the factored polynomial.\newline(x+7)(x+4)(x + 7)(x + 4)\newlineWrite your answer as a list of values separated by commas.\newlinex=x = ____
Get tutor helpright-arrow

Posted 9 months ago

View all (244)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant