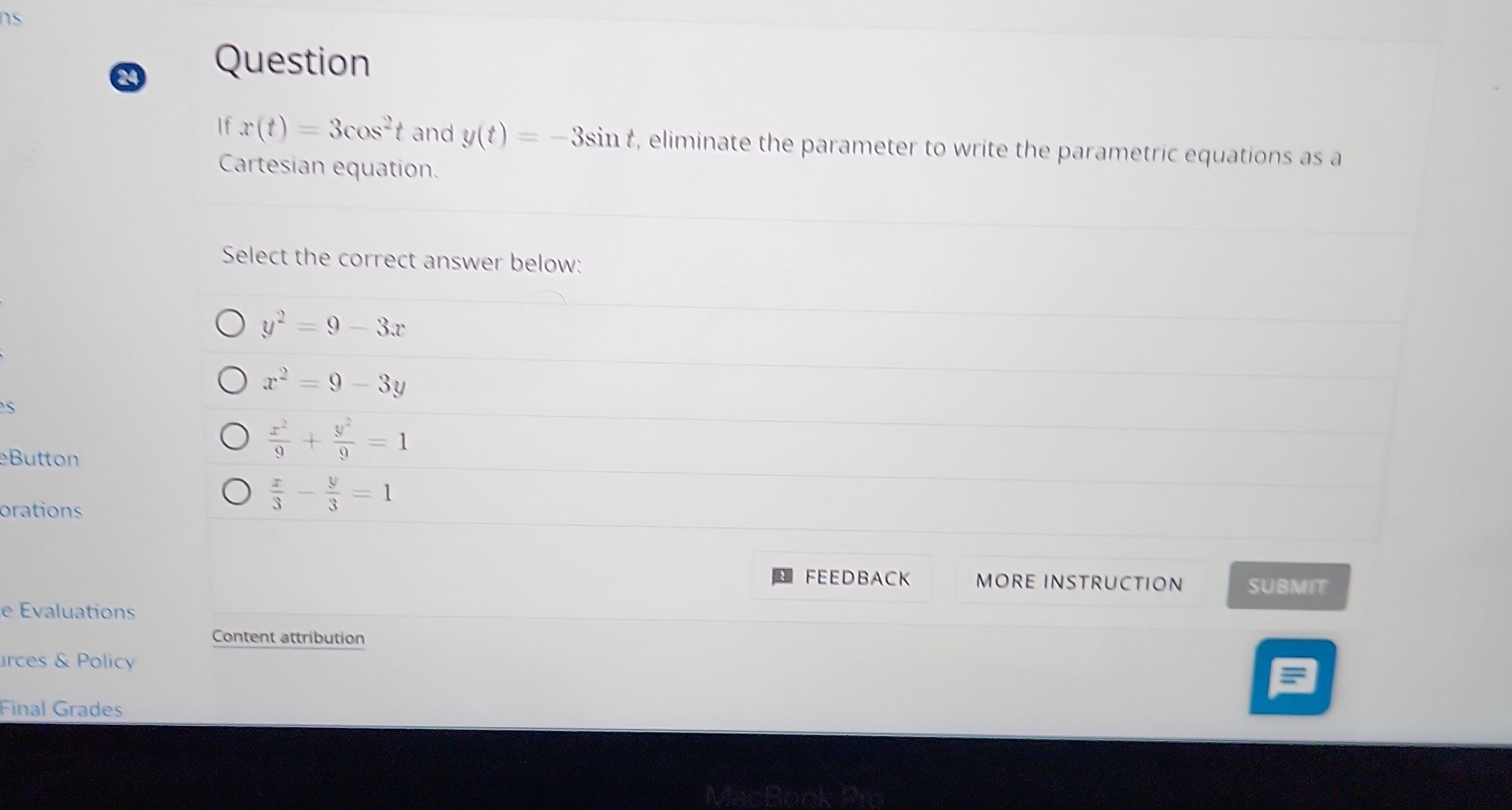
If x(t)=3cos^(2)t and y(t)=-3sin t, eliminate the parameter to write the parametric equations as a Cartesian equation. Select the correct answer below: (A) y^(2)=9-3x (B) x^(2)=9-3y (C) (x^(2))/(9)+(y^(2))/(9)=1 (D) (x)/(3)-(y)/(3)=1

Question

Bytelearn · Accepted Answer

Given Equations: Given the parametric equations: x(t) = 3cos^2(t) y(t) = -3sin(t) We want to eliminate the parameter t to find a Cartesian equation that relates x and y.Pythagorean Identity: We know that sin^2(t) + cos^2(t) = 1 from the Pythagorean identity.Expressing cos^2(t): We can express cos^2(t) in terms of x by rearranging the equation for x(t): x = 3cos^2(t) cos^2(t) = x/3Expressing sin(t): Similarly, we can express sin(t) in terms of y by rearranging the equation for y(t): y = -3sin(t) sin(t) = -y/3Squaring sin(t): Now we square both sides of the equation for sin(t) to get sin^2(t): sin^2(t) = (-y/3)^2 sin^2(t) = y^2/9Substitute into Identity: Substitute cos^2(t) and sin^2(t) into the Pythagorean identity: sin^2(t) + cos^2(t) = 1 (y^2/9) + (x/3) = 1Clearing Denominators: Multiply through by 9 to clear the denominators: 9(y^2/9) + 9(x/3) = 9(1) y^2 + 3x = 9Rearranging Equation: Rearrange the equation to match the answer choices: y^2 = 9 - 3x

Full solution

More problems from One-step inequalities: word problems

Related topics