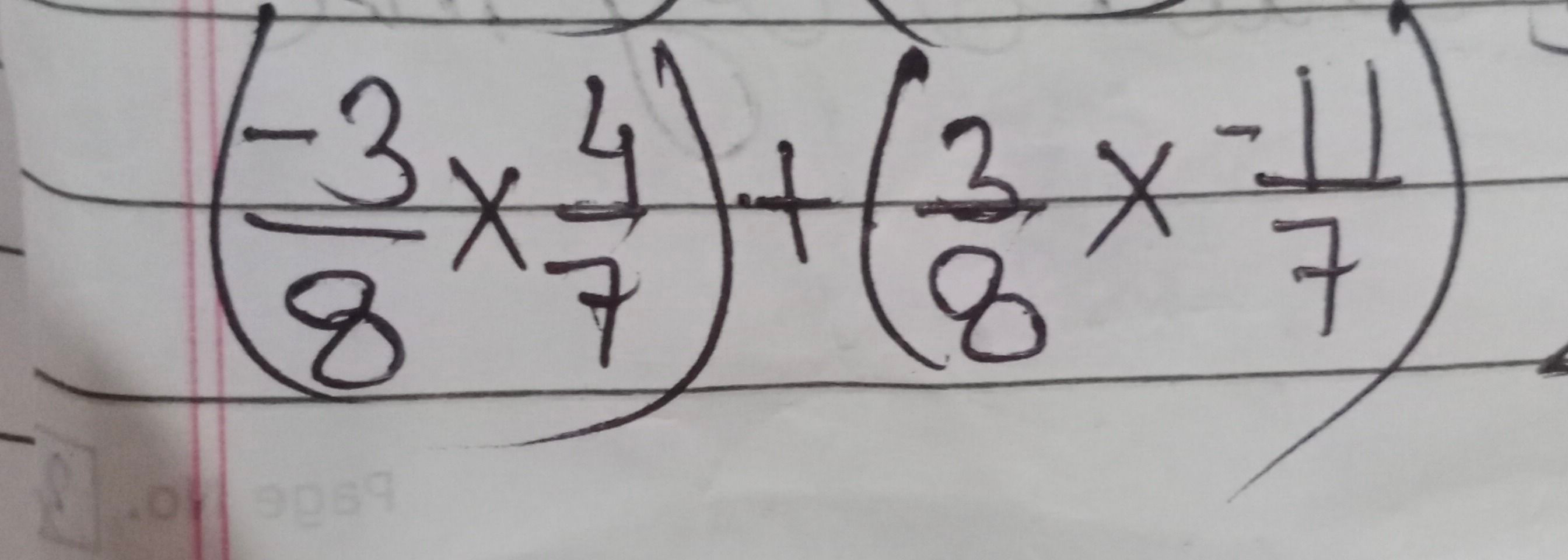((-3)/(8)×(4)/(7))+((3)/(8)×(-11)/(7))

Question

Bytelearn · Accepted Answer

Calculate Product of Fractions: Calculate the product of the first pair of fractions. We need to multiply the numerators together and the denominators together. (-3/8)×(4/7) = (-3×4)/(8×7) = -12/56 Now we simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor, which is 4. -12/56 = (-12÷4)/(56÷4) = -3/14Calculate Second Product: Calculate the product of the second pair of fractions. Similarly, we multiply the numerators together and the denominators together. (3/8)×(-11/7) = (3×-11)/(8×7) = -33/56 We can see that this fraction is already in its simplest form because 33 and 56 have no common divisors other than 1.Add Products Together: Add the two products together. Now we add the simplified fractions from Step 1 and Step 2. -3/14 + (-33/56) To add these fractions, we need a common denominator. The least common denominator (LCD) for 14 and 56 is 56. We need to convert -3/14 to a fraction with a denominator of 56. -3/14 = (-3×4)/(14×4) = -12/56 Now we can add the two fractions since they have the same denominator. -12/56 + (-33/56) = (-12 - 33)/56 = -45/56 This fraction is already in its simplest form because 45 and 56 have no common divisors other than 1.

$\left(\frac{-3}{8} \times \frac{4}{7}\right)+\left(\frac{3}{8} \times \frac{-11}{7}\right)$

Full solution

More problems from Add, subtract, multiply, and divide polynomials

Related topics

(−38×47)+(38×−117) \left(\frac{-3}{8} \times \frac{4}{7}\right)+\left(\frac{3}{8} \times \frac{-11}{7}\right) (8−3​×74​)+(83​×7−11​)

$\left(\frac{-3}{8} \times \frac{4}{7}\right)+\left(\frac{3}{8} \times \frac{-11}{7}\right)$