Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

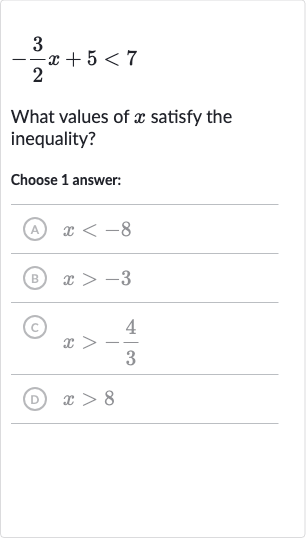
-(3)/(2)x+5 < 7 What values of x satisfy the inequality? Choose 1 answer: (A) x < -8 (B) x > -3 (c) x > -(4)/(3) (D) x > 8

-\frac{3}{2} x+5<7 \newlineWhat values of x x satisfy the inequality?\newlineChoose 11 answer:\newline(A) x<-8 \newline(B) x>-3 \newline(C) x>-\frac{4}{3} \newline(D) x>8

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Solve quadratic inequalitiesright chevron icon

Full solution

Q. −32x+5<7 -\frac{3}{2} x+5<7 \newlineWhat values of x x satisfy the inequality?\newlineChoose 11 answer:\newline(A) x<−8 x<-8 \newline(B) x>−3 x>-3 \newline(C) x>−43 x>-\frac{4}{3} \newline(D) x>8 x>8
  1. Isolate the term: Isolate the term containing xx on one side of the inequality.\newlineSubtract 55 from both sides of the inequality -\frac{3}{2}x + 5 < 7.\newline-\frac{3}{2}x + 5 - 5 < 7 - 5\newline-\frac{3}{2}x < 2
  2. Solve for x: Solve for x by dividing both sides of the inequality by −(3)/(2)-(3)/(2).\newlineRemember that dividing by a negative number reverses the inequality sign.\newlinex > 2 / (-(3)/(2))\newlinex > 2 \cdot (-2/3)\newlinex > -4/3
  3. Compare the solution: Compare the solution to the answer choices.\newlineThe solution x > -\frac{4}{3} matches with choice (C) x > -\left(\frac{4}{3}\right).

More problems from Solve quadratic inequalities

Question
Solve for ss.\newline∣s∣+3≥8|s| + 3 \geq 8
Get tutor helpright-arrow

Posted 4 months ago

Question
Which compound inequality represents the value of x?x ? \newline(x−1)(x+1)>0(x - 1)(x + 1) > 0\newline
Get tutor helpright-arrow

Posted 4 months ago

Question
A particular company charges advertisers a one time cost of $500\$500, in addition to $4.50\$4.50 for every one thousand times an advertisement is shown on the company's webpage. An advertiser wants its ad to appear MM thousand times on the webpage, but does not want to spend more than $5,000\$5,000. Which of the following inequalities best describes the situation? \newlineChoices: \newline(A) 500+4.50M≥5,000500+4.50M\geq5,000 \newline(B) 4.50+500M>5,0004.50+500M>5,000 \newline(C) 500+4.50M≤5,000500+4.50M\leq5,000 \newline(D) 500+4.50M<5,000500+4.50M<5,000
Get tutor helpright-arrow

Posted 7 months ago

Question
7x+1<x+97x+1 < x+9\newlineWhich of the following best describes the solutions to the inequality shown?\newlineChoose 11 answer:\newline(A) x>43x > \frac{4}{3}\newline(B) x<43x < \frac{4}{3}\newline(C) x<1x < 1\newline(D) x<53x < \frac{5}{3}
Get tutor helpright-arrow

Posted 4 months ago

Question
52−3x<−1452-3x < -14\newlineWhich of the following best describes the solutions to the inequality shown?\newlineChoose 11 answer:\newline(A) x>−383x > -\frac{38}{3}\newline(B) x>383x > \frac{38}{3}\newline(C) x<22x < 22\newline(D) x>22x > 22
Get tutor helpright-arrow

Posted 10 months ago

Question
5−3x>2x+25-3x > 2x+2\newlineWhich of the following best describes the solutions to the inequality shown?\newlineChoose 11 answer:\newline(A) x<75x < \frac{7}{5}\newline(B) x<3x < 3\newline(C) x<35x < \frac{3}{5}\newline(D) x>35x > \frac{3}{5}
Get tutor helpright-arrow

Posted 10 months ago

Question
Rani is a real estate agent. For each house she sells, she pays $100 \$ 100 in fees, but earns a commission of 1.8% 1.8 \% of the selling price of the house. Rani's total profit from a particular house is $4,580 \$ 4,580 . If p p represents the selling price of the house, which equation best models the situation?\newlineChoose 11 answer:\newline(A) 0.018p−100=4580 0.018 p-100=4580 \newline(B) 0.018p+100=4580 0.018 p+100=4580 \newline(C) (100−0.018)p=4580 (100-0.018) p=4580 \newline(D) (100+0.018)p=4580 (100+0.018) p=4580
Get tutor helpright-arrow

Posted 8 months ago

Question
A commercial airplane that is 11,500500 miles into a 22,500500 -mile journey is traveling at 450450 knots in still air when it picks up a tailwind of 150150 knots (in the same direction). If h h is the number of hours remaining in the airplane's flight, which of the following equations best describes the situation?\newline11 knot=1.15\mathrm{knot}=1.15 miles per hour (mph)\newlineChoose 11 answer:\newline(A) 1,500+690h=2,500 1,500+690 h=2,500 \newline(B) 1,500+600h=2,500 1,500+600 h=2,500 \newline(C) 1,500−600h=2,500 1,500-600 h=2,500 \newline(D) 1,500−690h=2,500 1,500-690 h=2,500
Get tutor helpright-arrow

Posted 7 months ago

Question
A weeping willow that is 1515 feet in height grows to a maximum height of 3535 feet in y y years at a constant rate of 2424 inches per year. Which of the following equations best describes this situation?\newline11 foot =12 =12 inches\newlineChoose 11 answer:\newline(A) 35=15+2y 35=15+2 y \newline(B) 35=15+24y 35=15+24 y \newline(C) 35=15−2y 35=15-2 y \newline(D) 35=15−24y 35=15-24 y
Get tutor helpright-arrow

Posted 10 months ago

Question
The gas mileage for a car is 2323 miles per gallon when the car travels at 6060 miles per hour. The car begins a trip with 1313 gallons in its tank, travels at an average speed of 6060 miles per hour for h h hours, and ends the trip with 1010 gallons in its tank. Which of the following equations best models this situation?\newlineChoose 11 answer:\newline(A) 13−23h60=10 13-\frac{23 h}{60}=10 \newline(B) 13−60h23=10 13-\frac{60 h}{23}=10 \newline(C) 13−60h23=10 \frac{13-60 h}{23}=10 \newline(D) 13−23h60=10 \frac{13-23 h}{60}=10
Get tutor helpright-arrow

Posted 8 months ago

View all (126)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant