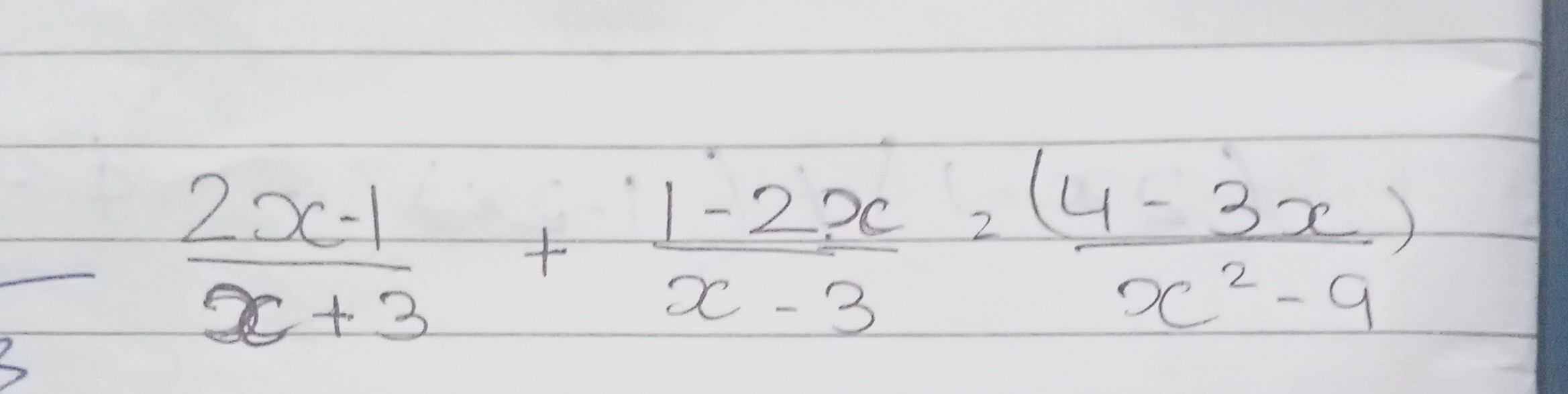Solve the equation. (2x-1)/(x+3)+(1-2x)/(x-3)=((4-3x))/(x^(2)-9)

Question

Bytelearn · Accepted Answer

Identify Common Denominator: Identify the common denominator for the two fractions. The denominators are (x+3) and (x-3). The common denominator will be the product of these two, which is (x+3)(x-3) or x^2 - 9.Rewrite with Common Denominator: Rewrite each fraction with the common denominator. (2x-1)/(x+3) becomes ((2x-1)(x-3))/(x^2-9) and (1-2x)/(x-3) becomes ((1-2x)(x+3))/(x^2-9).Expand Numerators: Expand the numerators of both fractions. For the first fraction: (2x-1)(x-3) = 2x(x) - 2x(3) - 1(x) + 1(3) = 2x^2 - 6x - x + 3 = 2x^2 - 7x + 3. For the second fraction: (1-2x)(x+3) = 1(x) + 1(3) - 2x(x) - 2x(3) = x + 3 - 2x^2 - 6x = -2x^2 - 5x + 3.Combine over Common Denominator: Combine the expanded numerators over the common denominator. (2x^2 - 7x + 3 - 2x^2 - 5x + 3) / (x^2 - 9).Simplify Combined Numerator: Simplify the combined numerator. 2x^2 - 7x + 3 - 2x^2 - 5x + 3 simplifies to -12x + 6.Write Simplified Expression: Write the simplified expression. The simplified form of the expression is (-12x + 6) / (x^2 - 9).Check Match with Given Expression: Check if the simplified expression matches the given expression on the right side of the equation. The given expression on the right side of the equation is (4-3x) / (x^2 - 9). This does not match our simplified expression (-12x + 6) / (x^2 - 9).

Solve the equation. $\newline$ $\frac{2 x-1}{x+3}+\frac{1-2 x}{x-3}=\frac{(4-3 x)}{x^{2}-9}$

Full solution

More problems from Add, subtract, multiply, and divide polynomials

Related topics

Solve the equation.\newline2x−1x+3+1−2xx−3=(4−3x)x2−9 \frac{2 x-1}{x+3}+\frac{1-2 x}{x-3}=\frac{(4-3 x)}{x^{2}-9} x+32x−1​+x−31−2x​=x2−9(4−3x)​

Solve the equation. $\newline$ $\frac{2 x-1}{x+3}+\frac{1-2 x}{x-3}=\frac{(4-3 x)}{x^{2}-9}$