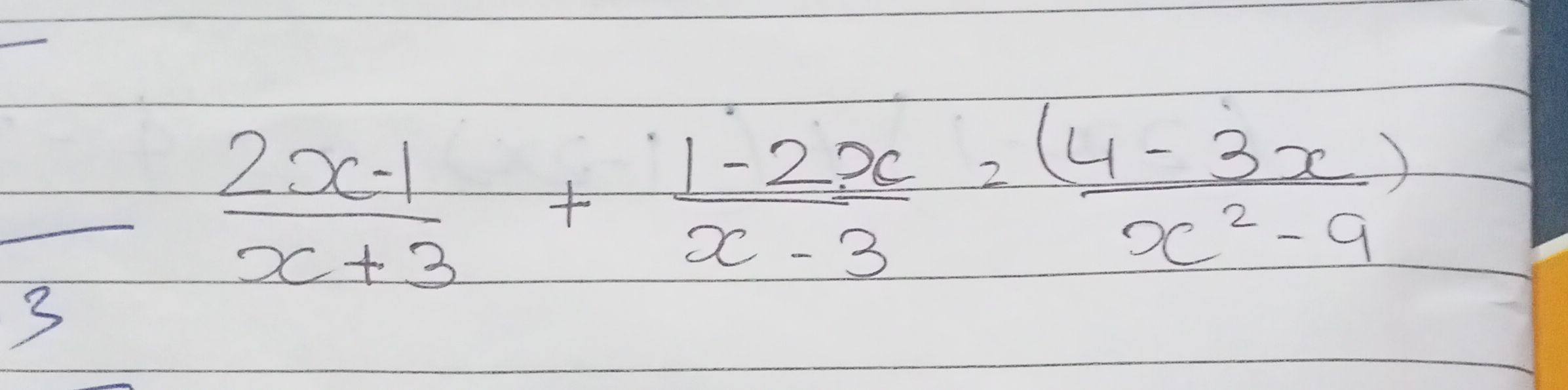Solve the equation. (2x-1)/(3)+(1-2x)/(x-3)=((4-3x))/(x^(2)-9)

Question

Bytelearn · Accepted Answer

Identify Common Denominator: Identify the common denominator for the fractions on the left side of the equation. The common denominator for the fractions (2x-1)/3 and (1-2x)/(x-3) is 3(x-3).Rewrite with Common Denominator: Rewrite each fraction with the common denominator. (2x-1)/3 * (x-3)/(x-3) + (1-2x)/(x-3) * 3/3 = ((4-3x))/(x^2-9) This gives us ((2x-1)(x-3))/3(x-3) + 3(1-2x)/3(x-3).Simplify Numerators: Simplify the numerators of the new fractions. ((2x-1)(x-3))/3(x-3) + 3(1-2x)/3(x-3) = (2x^2 - 6x - x + 3)/3(x-3) + (3 - 6x)/3(x-3) = (2x^2 - 7x + 3)/3(x-3) + (3 - 6x)/3(x-3)Combine Numerators: Combine the numerators over the common denominator. (2x^2 - 7x + 3 + 3 - 6x)/3(x-3) = (2x^2 - 13x + 6)/3(x-3)Factor Denominator: Notice that the right side of the equation has the denominator x^2 - 9, which factors to (x+3)(x-3). We can now equate the numerators since the denominators are the same. (2x^2 - 13x + 6) = (4 - 3x)Solve Equation: Solve the equation (2x^2 - 13x + 6) = (4 - 3x) by moving all terms to one side. 2x^2 - 13x + 6 - 4 + 3x = 0 2x^2 - 10x + 2 = 0Simplify Equation: Simplify the equation by dividing all terms by 2. x^2 - 5x + 1 = 0Use Quadratic Formula: This is a quadratic equation, which can be solved by factoring, completing the square, or using the quadratic formula. However, this equation does not factor nicely, so we will use the quadratic formula. x = [-(-5) ± √((-5)^2 - 4(1)(1))]/(2(1)) x = [5 ± √(25 - 4)]/2 x = [5 ± √21]/2

Solve the equation. $\newline$ $\frac{2 x-1}{3}+\frac{1-2 x}{x-3}=\frac{(4-3 x)}{x^{2}-9}$

Full solution

More problems from Add, subtract, multiply, and divide polynomials

Related topics

Solve the equation.\newline2x−13+1−2xx−3=(4−3x)x2−9 \frac{2 x-1}{3}+\frac{1-2 x}{x-3}=\frac{(4-3 x)}{x^{2}-9} 32x−1​+x−31−2x​=x2−9(4−3x)​

Solve the equation. $\newline$ $\frac{2 x-1}{3}+\frac{1-2 x}{x-3}=\frac{(4-3 x)}{x^{2}-9}$