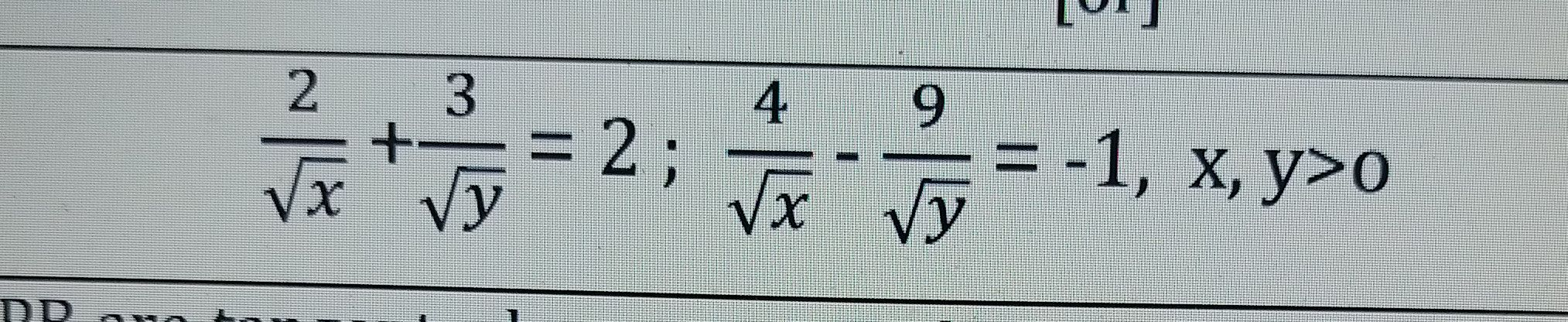(2)/(sqrtx)+(3)/(sqrty)=2;(4)/(sqrtx)-(9)/(sqrty)=-1,x,y 0

Question

(2)/(sqrtx)+(3)/(sqrty)=2;(4)/(sqrtx)-(9)/(sqrty)=-1,x,y > 0

Bytelearn · Accepted Answer

Substitution of Variables: Let's denote u = 1/sqrt(x) and v = 1/sqrty. This substitution will simplify the equations since we will be dealing with linear terms instead of rational expressions.Rewriting First Equation: Rewrite the first equation using the new variables u and v: 2u + 3v = 2.Rewriting Second Equation: Rewrite the second equation using the new variables u and v: 4u - 9v = -1.System of Linear Equations: Now we have a system of linear equations: 2u + 3v = 2, 4u - 9v = -1. We can solve this system using the method of substitution or elimination. Let's use the elimination method.Multiplying First Equation: Multiply the first equation by 2 to make the coefficients of u the same in both equations: (2u + 3v) * 2 = 2 * 2, which gives us 4u + 6v = 4.Subtracting Equations: Now subtract the second equation from the new equation obtained in the previous step: (4u + 6v) - (4u - 9v) = 4 - (-1), which simplifies to 15v = 5.Solving for v: Divide both sides of the equation by 15 to solve for v: 15v / 15 = 5 / 15, which gives us v = 1/3.Substituting Back for u: Now that we have the value of v, we can substitute it back into one of the original equations to solve for u. Let's use the first equation: 2u + 3(1/3) = 2, which simplifies to 2u + 1 = 2.Solving for u: Subtract 1 from both sides of the equation to solve for u: 2u + 1 - 1 = 2 - 1, which gives us 2u = 1.Finding x and y: Divide both sides of the equation by 2 to solve for u: 2u / 2 = 1 / 2, which gives us u = 1/2.Substitute Values for x and y: Now that we have the values of u and v, we can find the values of x and y by reversing the substitution we made at the beginning: u = 1/sqrt(x) implies sqrt(x) = 1/u, v = 1/sqrty implies sqrty = 1/v.Calculating x and y: Substitute the values of u and v to find x and y: sqrt(x) = 1/(1/2) implies x = (1/(1/2))^2, sqrty = 1/(1/3) implies y = (1/(1/3))^2.Calculate the values of x and y: x = (2/1)^2 = 4, y = (3/1)^2 = 9.

\frac{2}{\sqrt{x}}+\frac{3}{\sqrt{y}}=2 ; \frac{4}{\sqrt{x}}-\frac{9}{\sqrt{y}}=-1, \mathrm{x}, \mathrm{y}>0

Full solution

More problems from Solve multi-step equations with fractional coefficients

Related topics