Full solution
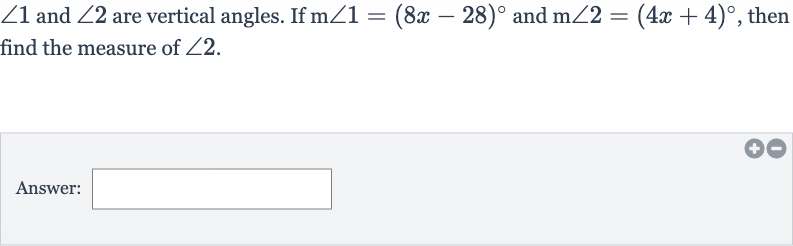
Q. and are vertical angles. If and , then find the measure of .Answer:
- Set Equal Expressions: Vertical angles are congruent, which means they have equal measures. Therefore, we can set the expressions for and equal to each other to find the value of .Equation:
- Subtract x Terms: Now, we will solve for by first subtracting from both sides of the equation to get the terms on one side.
- Add : Next, we will add to both sides of the equation to isolate the term.
- Divide by : Now, we will divide both sides of the equation by to solve for .
- Substitute x Value: With the value of found, we can now substitute it back into the expression for to find its measure. degrees
More problems from Transformations of functions
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help