Full solution
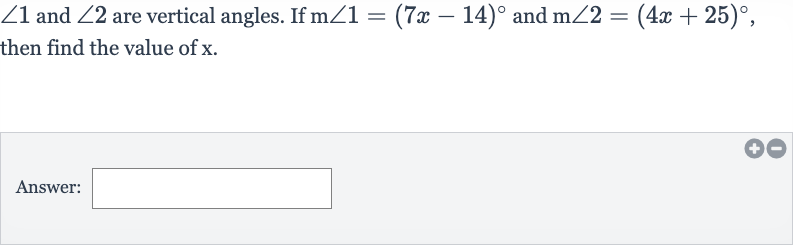
Q. and are vertical angles. If and , then find the value of .Answer:
- Set Angle Expressions Equal: Vertical angles are congruent, which means they have equal measures. Therefore, we can set the expressions for and equal to each other to find the value of .
- Subtract : Subtract from both sides to start isolating the variable on one side of the equation.This simplifies to:
- Add : Add to both sides to further isolate .This simplifies to:
- Divide by : Divide both sides by to solve for .This simplifies to: