Full solution
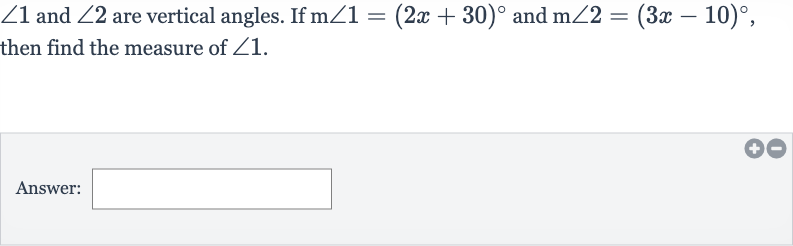
Q. and are vertical angles. If and , then find the measure of .Answer:
- Vertical Angles Congruent: Vertical angles are congruent, which means they have the same measure. Therefore, we can set the expressions for and equal to each other to find the value of . = \)
- Solve for x: Now, we solve for x by subtracting from both sides of the equation.
- Isolate x: Next, we add to both sides of the equation to isolate .
- Substitute into Angle : Now that we have the value of , we can substitute it back into the expression for to find the measure of angle .
- Find Measure of Angle : Finally, we perform the multiplication and addition to find the measure of angle .m/angle = m/angle = degrees