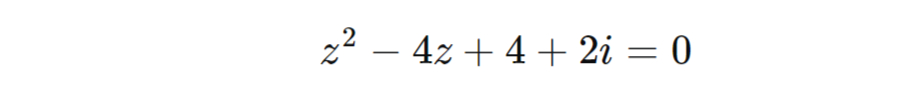AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
Solve for .
Full solution
Q. Solve for .
- Identify Quadratic Equation: Step Title: Identify the Quadratic EquationConcise Step Description: Recognize the given equation as a quadratic equation in the complex number system.Step Calculation: The given equation is .Step Output: Quadratic Equation:
- Complete the Square: Step Title: Complete the SquareConcise Step Description: Complete the square for the quadratic equation to find the roots.Step Calculation: . Group the real coefficients: . Recognize that is a perfect square trinomial.. Factor the perfect square trinomial: Step Output: Factored Form:
- Solve for z: Step Title: Solve for zConcise Step Description: Solve the factored equation for z.Step Calculation: . Isolate the perfect square: . Take the square root of both sides: . Solve for z: Step Output: Roots:
- Simplify Square Root: Step Title: Simplify the Square Root of the Complex NumberConcise Step Description: Simplify the square root of the complex number -2i＂).\(\newlineStep Calculation: 1. Recognize that \$\sqrt{-2i} = \sqrt{2} \times \sqrt{-i}\)\(\newline\)\(2\). Since \(\sqrt{-i} = i\sqrt{i}\) and \(\sqrt{i} = \frac{1 + i}{\sqrt{2}}\) (using the principal square root), we have \(\sqrt{-2i} = \sqrt{2} \times i \times \frac{1 + i}{\sqrt{2}}\)\(\newline\)\(3\). Simplify the expression: \(\sqrt{-2i} = i(1 + i)\)\(\newline\)\(4\). Multiply out: \(\sqrt{-2i} = i + i^2\)\(\newline\)\(5\). Since \(i^2 = -1\), we get: \(\sqrt{-2i} = i - 1\)\(\newline\)Step Output: Simplified Square Root: \(\sqrt{-2i} = i - 1\)
- Find Final Roots: Step Title: Find the Final Roots\(\newline\)Concise Step Description: Substitute the simplified square root back into the roots equation.\(\newline\)Step Calculation: \(\newline\)\(1\). Substitute \(\sqrt{-2i}\) with \(i - 1\) in the roots equation: \(z = 2 \pm (i - 1)\)\(\newline\)\(2\). Write out the two roots: \(z = 2 + i - 1\) and \(z = 2 - i + 1\)\(\newline\)\(3\). Simplify both roots: \(z = 1 + i\) and \(z = 3 - i\)\(\newline\)Step Output: Final Roots: \(z = 1 + i\) and \(z = 3 - i\)
More problems from Factor polynomials
QuestionGet tutor help
QuestionGet tutor help