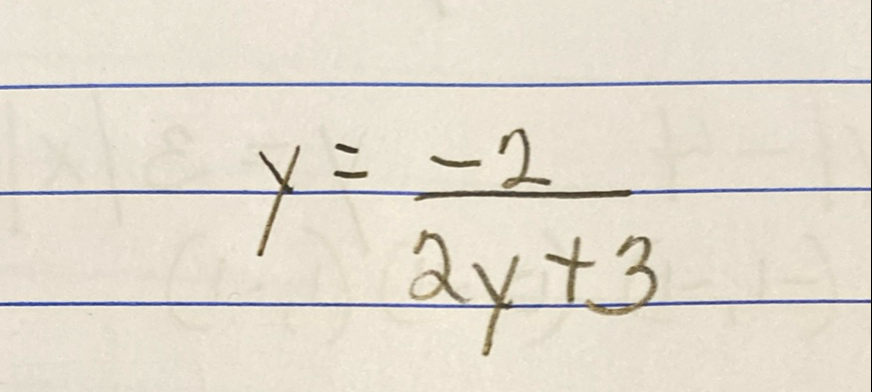AI tutor
Full solution
Q.
- Start with the equation: We start with the equation: Our goal is to solve for .
- Multiply to eliminate fraction: To eliminate the fraction, we multiply both sides of the equation by to get:
- Distribute on left side: Distribute on the left side of the equation:
- Set equation to zero: We want to set the equation to zero to solve for , so we add to both sides:
- Factor the quadratic equation: Now we have a quadratic equation. We can attempt to factor it, or use the quadratic formula. Let's try factoring first:
- Solve for in first equation: Set each factor equal to zero and solve for : or
- Solve for in second equation: Solve the first equation for :
- Solve for y in second equation: Solve the first equation for y:Solve the second equation for y:
More problems from Evaluate integers raised to rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help