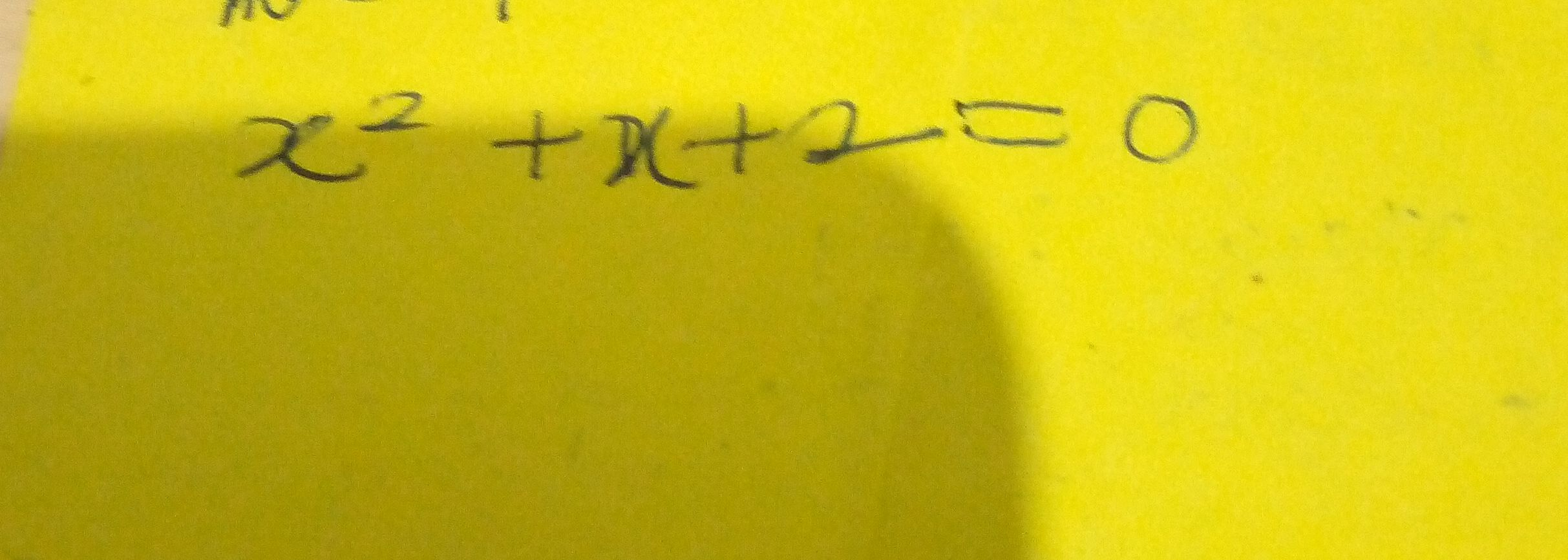AI tutor
Full solution
Q.
- Identify Equation Type: Identify the type of equation.The given equation is a quadratic equation in the standard form , where , , and .
- Apply Quadratic Formula: Apply the quadratic formula to find the solutions.The quadratic formula is . For our equation, , , and .
- Calculate Discriminant: Calculate the discriminant.The discriminant is the part of the quadratic formula under the square root: . Let's calculate it: .
- Determine Root Nature: Determine the nature of the roots.Since the discriminant is negative , the equation has two complex solutions.
- Calculate Solutions: Calculate the solutions using the quadratic formula. , where is the imaginary unit.
- Write Final Solutions: Write the final solutions.The solutions to the equation are and .
More problems from Solve complex trigonomentric equations
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help