Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

x^(2)+kx-14=0
In the given equation,
k is a constant. The equation has solutions at 7 and -2 . What is the value of
k ?
Choose 1 answer:
(A) -9
(B) -5
(C) 5
(D) 9

$x^{2}+kx-14=0$ $\newline$ In the given equation, $k$ is a constant. The equation has solutions at $7$ and $-2$ . What is the value of $k$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $-9$ $\newline$ (B) $-5$ $\newline$ (C) $5$ $\newline$ (D) $9$

View step-by-step help

View step-by-step help

Solve trigonometric equations

Full solution

Q.

x^{2}+kx-14=0

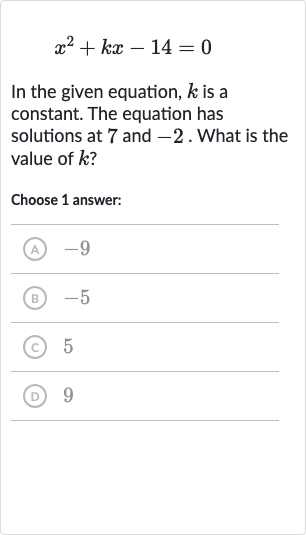
\newline

In the given equation,

k

is a constant. The equation has solutions at

7

and

-2

. What is the value of

k

?

\newline

Choose

1

answer:

\newline

(A)

-9

\newline

(B)

-5

\newline

(C)

5

\newline

(D)

9

Relationships between coefficients: Since the solutions to the quadratic equation are given as $7$ and $-2$ , we can use the fact that the solutions to a quadratic equation of the form $ax^2 + bx + c = 0$ are related to the coefficients by the relationships sum of roots = $-b/a$ and product of roots = $c/a$ . In this case, $a = 1$ , so the sum of the roots is $-k/1$ and the product of the roots is $-14/1$ .
Calculate sum of roots: The sum of the roots is $7 + (-2) = 5$ . According to the relationship sum of roots $= -b/a$ , we have $5 = -k/1$ . Therefore, $k = -5$ .
Calculate product of roots: The product of the roots is $7 \times (-2) = -14$ . According to the relationship product of roots $= \frac{c}{a}$ , we have $-14 = \frac{-14}{1}$ . This confirms that the product of the roots is consistent with the constant term of the quadratic equation.
Determine value of $k$ : Since the sum of the roots is $5$ and we have found that $k = -5$ , we can conclude that the value of $k$ is indeed $-5$ . This corresponds to option (B) in the given choices.

More problems from Solve trigonometric equations

Question

Find all solutions with

0^\circ \leq \theta \leq 180^\circ

. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.

\newline

\cos(\theta) = -1

\newline

\underline{\hspace{2em}}^\circ

Posted 7 months ago

Question

Kimi's school is

15

kilometers west of her house and

8

kilometers south of her friend Franklin's house. Every day, Kimi bicycles from her house to her school. After school, she bicycles from her school to Franklin's house. Before dinner, she bicycles home on a bike path that goes straight from Franklin's house to her own house. How far does Kimi bicycle each day?

\newline

\_\_\_\_\_

Posted 7 months ago

Question

Evaluate. Write your answer as an integer or as a decimal rounded to the nearest hundredth.

\newline

\cos 35^\circ =

Posted 7 months ago

Question

Find all solutions with

-90^\circ \leq \theta \leq 90^\circ

. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.

\newline

\csc(\theta) = -1

\newline

\_\_\_\_\,^\circ

Posted 8 months ago

Question

Evaluate. Write your answer in simplified, rationalized form. Do not round.

\newline

\cot 30^\circ =

Posted 7 months ago

Question

The terminal side of an angle

\theta

in standard position intersects the unit circle at

(\frac{84}{85}, \frac{13}{85})

\cos(\theta)

\newline

Write your answer in simplified, rationalized form.

\newline

Posted 7 months ago

Question

-90^\circ < \theta < 90^\circ

. Find the value of

\theta

\newline

\tan(\theta) = 0

\newline

Write your answer in simplified, rationalized form. Do not round.

\newline

\theta =

^\circ

\newline

Posted 8 months ago

Question

Evaluate. Write your answer in simplified, rationalized form. Do not round.

\newline

\csc 60^\circ =

Posted 8 months ago

Question

\theta

is an acute angle. Find the value of

\theta

\newline

\sec(\theta) = \sqrt{2}

\newline

\theta =

\degree

Posted 7 months ago

Question

Evaluate. Write your answer in simplified, rationalized form. Do not round.

\newline

\cos 90^\circ =

Posted 9 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant