AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
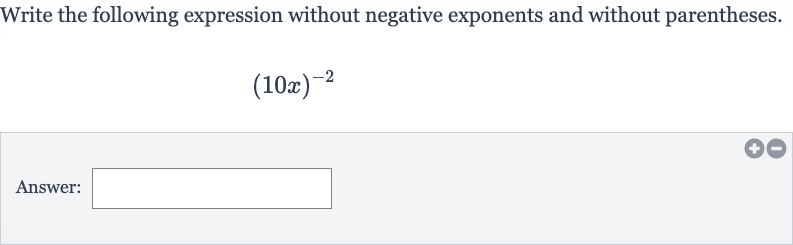
Write the following expression without negative exponents and without parentheses.Answer:
Full solution
Q. Write the following expression without negative exponents and without parentheses.Answer:
- Use Rule for Negative Exponents: To remove the negative exponent, we can use the rule that , where is the base and is the exponent. This means we need to take the reciprocal of the base when the exponent is negative.
- Apply Rule to : Applying this rule to , we get . This removes the negative exponent.
- Square the Base: Now we need to square the base, which means we will square both and . So becomes .
- Calculate Final Expression: Calculating gives us . So we have , which is the expression without negative exponents and without parentheses.
