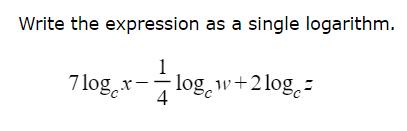AI tutor
Full solution
Q. Write the expression as a single logarithm.
- Apply Power Rule: We are given the expression . To combine these logarithms into a single logarithm, we will use the logarithm properties: the power rule, which states that , and the product and quotient rules, which state that and , respectively.
- Rewrite Using Rules: First, apply the power rule to each term to move the coefficients inside the logarithms as exponents of the arguments. becomes becomes becomes
- Combine Terms: Now, rewrite the expression using the product and quotient rules.According to the product rule, we can combine the terms with addition into a single logarithm with a product inside.And according to the quotient rule, we can combine the term with subtraction into a single logarithm with a quotient inside.
- Final Answer: The expression is now simplified to a single logarithm: This is the final answer.
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help