Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

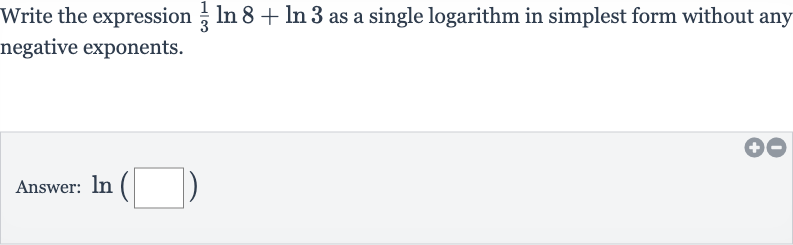
Write the expression
(1)/(3)ln 8+ln 3 as a single logarithm in simplest form without any negative exponents.
Answer:
ln(◻)

Write the expression $\frac{1}{3} \ln 8+\ln 3$ as a single logarithm in simplest form without any negative exponents. $\newline$ Answer: $\ln (\square)$

View step-by-step help

View step-by-step help

Power rule with rational exponents

Full solution

Q. Write the expression

\frac{1}{3} \ln 8+\ln 3

as a single logarithm in simplest form without any negative exponents.

\newline

Answer:

\ln (\square)

Apply Power Rule: We have the expression $(\frac{1}{3})\ln 8 + \ln 3$ . To combine these logarithms into a single logarithm, we can use the logarithm properties.
Simplify $8^{1/3}$ : First, we apply the power rule of logarithms, which states that $a \cdot \ln(b) = \ln(b^a)$ , to the term $(1/3)\ln 8$ . $\newline$ $(1/3)\ln 8 = \ln(8^{1/3})$
Substitute $2$ : Now we simplify $8^{1/3}$ . Since $8$ is $2^3$ , we can write $8^{1/3}$ as $(2^3)^{1/3}$ . $\newline$ $8^{1/3} = (2^3)^{1/3}$
Combine Logarithms: Using the power of a power rule, which states $(a^n)^m = a^{n*m}$ , we simplify $(2^3)^{1/3}$ . $(2^3)^{1/3} = 2^{3*(1/3)} = 2^1 = 2$
Calculate Product: Now we substitute $2$ back into the logarithm to get $\ln(2)$ . $\newline$ $\ln(8^{1/3}) = \ln(2)$
Write Final Expression: We now have $\ln(2) + \ln(3)$ . To combine these two logarithms into a single logarithm, we use the product rule of logarithms, which states $\ln(a) + \ln(b) = \ln(a*b)$ . $\newline$ $\ln(2) + \ln(3) = \ln(2*3)$
Write Final Expression: We now have $\ln(2) + \ln(3)$ . To combine these two logarithms into a single logarithm, we use the product rule of logarithms, which states $\ln(a) + \ln(b) = \ln(a*b)$ . $\ln(2) + \ln(3) = \ln(2*3)$ We calculate the product $2*3$ . $2*3 = 6$
Write Final Expression: We now have $\ln(2) + \ln(3)$ . To combine these two logarithms into a single logarithm, we use the product rule of logarithms, which states $\ln(a) + \ln(b) = \ln(a*b)$ . $\ln(2) + \ln(3) = \ln(2*3)$ We calculate the product $2*3$ . $2*3 = 6$ Finally, we write the expression as a single logarithm. $\ln(2*3) = \ln(6)$

More problems from Power rule with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 9 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 5 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 5 months ago

Question

\newline

32^{(-1/5)}

Posted 7 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant