Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

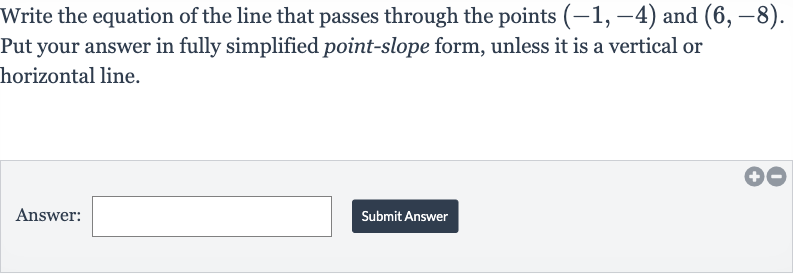
Write the equation of the line that passes through the points
(-1,-4) and
(6,-8). Put your answer in fully simplified point-slope form, unless it is a vertical or horizontal line.
Answer:
Submit Answer

Write the equation of the line that passes through the points $(-1,-4)$ and $(6,-8)$ . Put your answer in fully simplified point-slope form, unless it is a vertical or horizontal line. $\newline$ Answer: $\newline$ Submit Answer

View step-by-step help

View step-by-step help

Find the magnitude of a three-dimensional vector

Full solution

Q. Write the equation of the line that passes through the points

(-1,-4)

and

(6,-8)

. Put your answer in fully simplified point-slope form, unless it is a vertical or horizontal line.

\newline

Answer:

\newline

Submit Answer

Calculate the Slope: First, calculate the slope $m$ of the line using the formula $m = \frac{y_2 - y_1}{x_2 - x_1}$ , where $(x_1, y_1)$ and $(x_2, y_2)$ are the given points. $\newline$ $m = \frac{-8 - (-4)}{6 - (-1)}$ $\newline$ $m = \frac{-8 + 4}{6 + 1}$ $\newline$ $m = \frac{-4}{7}$
Use Point-Slope Form: Now that we have the slope, we can use the point-slope form of the line equation, which is $y - y_1 = m(x - x_1)$ . We can use either of the given points; let's use the first point $(-1, -4)$ . $\newline$ $y - (-4) = \frac{-4}{7}(x - (-1))$ $\newline$ $y + 4 = \frac{-4}{7}(x + 1)$
Simplify the Equation: Next, we simplify the equation. $\newline$ $y + 4 = \left(-\frac{4}{7}\right)x - \left(\frac{4}{7}\right)(1)$ $\newline$ $y + 4 = \left(-\frac{4}{7}\right)x - \frac{4}{7}$
Subtract to Simplify: To get the equation in point-slope form, we subtract $4$ from both sides. $\newline$ $y = \left(-\frac{4}{7}\right)x - \frac{4}{7} - 4$ $\newline$ $y = \left(-\frac{4}{7}\right)x - \frac{4}{7} - \frac{28}{7}$ $\newline$ $y = \left(-\frac{4}{7}\right)x - \frac{32}{7}$
Final Equation: The equation is now in point-slope form, and it is fully simplified.

More problems from Find the magnitude of a three-dimensional vector

Question

Rewrite in simplest terms:

6 c-9(-2 c-9)

\newline

Posted 6 months ago

Question

Find the coordinates of the vertex of the following parabola using graphing technology. Write your answer as an

(x, y)

\newline

y=-2 x^{2}-12 x-2

\newline

Posted 7 months ago

Question

Find the coordinates of the vertex of the following parabola algebraically. Write your answer as an

(x, y)

\newline

y=-2 x^{2}-18

\newline

Posted 7 months ago

Question

Find the distance between

P(4,4)

Q(9,7)

\newline

The distance between

P

Q

\square

\newline

(Simplify your answer. Type an exact answer using radicals as need

Posted 6 months ago

Question

Find the length and width op the quadrilateral with vertices at

(6,4),(4,4,(6,7),(4,7)

Posted 6 months ago

Question

\begin{aligned} x+y&=3, \ & x-3y=-9 \end{aligned}

\newline

What is the solution

(x,y)

to the given system of equations?

Posted 6 months ago

Question

6

. The length and breadth of a room are

3 x^{2} y^{3}

6 x^{3} y^{2}

. Find its and area.

Posted 6 months ago

Question

(2,58)

(9,72)

are two anchor points on a trend line, then find the equation of the line.

Posted 6 months ago

Question

Find an explicit formula for the geometric sequence 2\,,\,6\,,\,18\,,\,54,\unicode{0x2026}. Note: the first term should be

b(1)

Posted 6 months ago

Question

\frac{\left(\log _{x} 5+\log _{5} x-1\right)\left(\log _{x}(5 x)\right)}{1+\left(\log _{x} 5\right)^{3}}=\log _{125} 3

\newline

olduğuna göre,

x^{102}

6

ile bölümünden kalan kaçtır?

\newline

1

\newline

2

\newline

3

\newline

4

\newline

5

Posted 9 hours ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant