AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
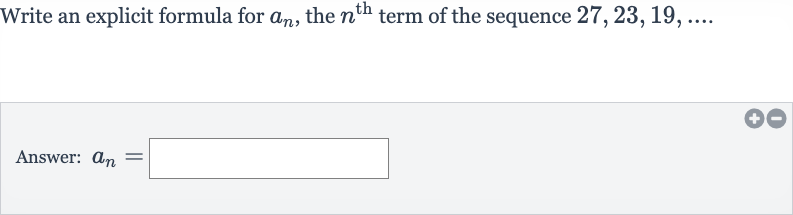
Write an explicit formula for , the term of the sequence .Answer:
Full solution
Q. Write an explicit formula for , the term of the sequence .Answer:
- Sequence Type: We have the sequence: Is the given sequence geometric or arithmetic?Here, there is a common difference between consecutive terms.The given sequence is arithmetic.
- Initial Values: Determine the values of and of the sequence.The first term, Common difference,
- Explicit Formula: We have:Write an explicit formula to describe the sequence
