Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

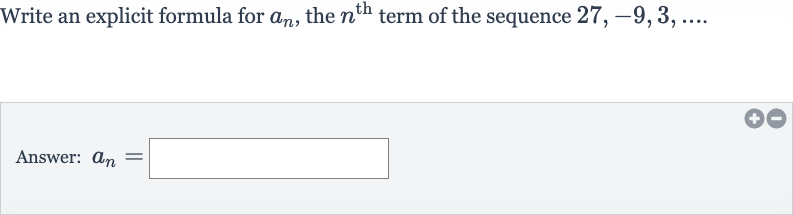
Write an explicit formula for
a_(n), the
n^("th ") term of the sequence
27,-9,3,dots
Answer:
a_(n)=

Write an explicit formula for $a_{n}$ , the $n^{\text {th }}$ term of the sequence $27,-9,3, \ldots$ $\newline$ Answer: $a_{n}=$

View step-by-step help

View step-by-step help

Convert between explicit and recursive formulas

Full solution

Q. Write an explicit formula for

a_{n}

, the

n^{\text {th }}

term of the sequence

27,-9,3, \ldots

\newline

Answer:

a_{n}=

Identify pattern in sequence: We first identify the pattern in the sequence. The sequence starts with $27$ and each term is divided by $-3$ to get the next term: $27, -9, 3, \ldots$
Calculate ratio: This is a geometric sequence because each term is obtained by multiplying the previous term by a constant ratio. To find the ratio $r$ , we divide the second term by the first term: $r = (-9) / 27 = -\frac{1}{3}$ .
Use geometric sequence formula: The first term of the sequence, $a_1$ , is $27$ . The $n$ th term of a geometric sequence is given by the formula $a_n = a_1 \times r^{(n-1)}$ , where $a_1$ is the first term and $r$ is the common ratio.
Substitute values into formula: Substituting the values of $a_1$ and $r$ into the formula, we get $a_n = 27 \times (-\frac{1}{3})^{(n-1)}$ .
Simplify if necessary: This is the explicit formula for the $n$ th term of the sequence. It can be simplified further if necessary, but in this case, it is already in its simplest form.

More problems from Convert between explicit and recursive formulas

Question

Find the sum of the finite arithmetic series.

\sum_{n=1}^{10} (7n+4)

\newline

Posted 3 months ago

Question

Type the missing number in this sequence: `55,\59,\63,\text{_____},\71,\75,\79`

Posted 2 months ago

Question

Type the missing number in this sequence: `2, 4 8`, ______,`32`

Posted 2 months ago

Question

What kind of sequence is this?

2, 10, 50, 250, \ldots

Choices:Choices:

\newline

\text{[A]arithmetic}

\newline

\text{[B]geometric}

\newline

\text{[C]both}

\newline

\text{[D]neither}

Posted 2 months ago

Question

What is the missing number in this pattern?

1, 4, 9, 16, 25, 36, 49, 64, 81, \_\_\_\_

Posted 2 months ago

Question

Classify the series.

\sum_{n = 0}^{12} (n + 2)^3

\newline

\newline

\text{[A]arithmetic}

\newline

\text{[B]geometric}

\newline

\text{[C]both}

\newline

\text{[D]neither}

Posted 2 months ago

Question

Find the first three partial sums of the series.

\newline

1 + 6 + 11 + 16 + 21 + 26 + \cdots

\newline

Write your answers as integers or fractions in simplest form.

\newline

S_1 =

\newline

S_2 =

\newline

S_3 =

Posted 2 months ago

Question

Find the third partial sum of the series.

\newline

3 + 9 + 15 + 21 + 27 + 33 + \cdots

\newline

Write your answer as an integer or a fraction in simplest form.

\newline

S_3 =

Posted 2 months ago

Question

Find the first three partial sums of the series.

\newline

1 + 7 + 13 + 19 + 25 + 31 + \cdots

\newline

Write your answers as integers or fractions in simplest form.

\newline

S_1 =

\newline

S_2 =

\newline

S_3 =

Posted 3 months ago

Question

Does the infinite geometric series converge or diverge?

\newline

1 + \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots

\newline

\newline

\text{[A]converge}

\newline

\text{[B]diverge}

Posted 2 months ago