AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
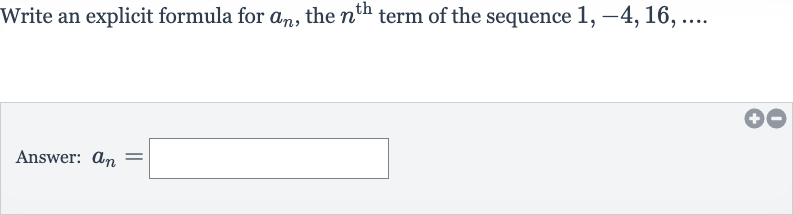
Write an explicit formula for , the term of the sequence Answer:
Full solution
Q. Write an explicit formula for , the term of the sequence Answer:
- Identify Pattern: Identify the pattern in the sequence.The given sequence is We notice that each term is multiplied by to get the next term.This indicates that the sequence is geometric.
- Determine Terms: Determine the first term and the common ratio of the sequence.The first term, To find the common ratio, , we divide the second term by the first term:
- Write Formula: Write the explicit formula for the nth term of a geometric sequence.The formula for the nth term of a geometric sequence is:Substitute the values of and into the formula:
- Simplify: Simplify the formula.The simplified formula for the nth term is:
