Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

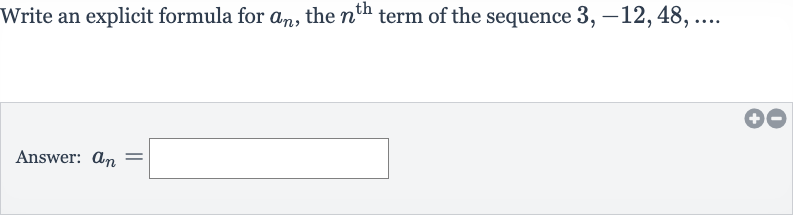
Write an explicit formula for a_(n), the n^("th ") term of the sequence 3,-12,48,dots Answer: a_(n)=

Write an explicit formula for an a_{n} , the nth  n^{\text {th }} term of the sequence 3,−12,48,… 3,-12,48, \ldots \newlineAnswer: an= a_{n}=

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Convert between explicit and recursive formulasright chevron icon

Full solution

Q. Write an explicit formula for an a_{n} , the nth  n^{\text {th }} term of the sequence 3,−12,48,… 3,-12,48, \ldots \newlineAnswer: an= a_{n}=
  1. Identify Pattern in Sequence: The first step is to identify the pattern in the sequence. We notice that each term is multiplied by −4-4 to get the next term. This indicates that the sequence is geometric with a common ratio of −4-4.
  2. Calculate nth Term Formula: The first term of the sequence, a1a_1, is 33. Since this is a geometric sequence, the nth term is given by the formula an=a1×r(n−1)a_n = a_1 \times r^{(n-1)}, where rr is the common ratio.
  3. Substitute Values into Formula: Substituting the known values into the formula, we get an=3×(−4)(n−1)a_n = 3 \times (-4)^{(n-1)}.
  4. Check Formula with First Terms: We should check the formula with the first few terms to ensure there are no mistakes. For n=1n=1, an=3×(−4)1−1=3×1=3a_n = 3 \times (-4)^{1-1} = 3 \times 1 = 3, which matches the first term of the sequence. For n=2n=2, an=3×(−4)2−1=3×(−4)=−12a_n = 3 \times (-4)^{2-1} = 3 \times (-4) = -12, which matches the second term of the sequence. For n=3n=3, an=3×(−4)3−1=3×16=48a_n = 3 \times (-4)^{3-1} = 3 \times 16 = 48, which matches the third term of the sequence. The formula appears to be correct.

More problems from Convert between explicit and recursive formulas

Question
Find the sum of the finite arithmetic series. ∑n=110(7n+4)\sum_{n=1}^{10} (7n+4)\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Type the missing number in this sequence: `55,\59,\63,\text{_____},\71,\75,\79`
Get tutor helpright-arrow

Posted 1 month ago

Question
Type the missing number in this sequence: `2, 4 8`, ______,`32`
Get tutor helpright-arrow

Posted 2 months ago

Question
What kind of sequence is this? 2,10,50,250,…2, 10, 50, 250, \ldots Choices:Choices:\newline[A]arithmetic\text{[A]arithmetic}\newline[B]geometric\text{[B]geometric}\newline[C]both\text{[C]both}\newline[D]neither\text{[D]neither}
Get tutor helpright-arrow

Posted 2 months ago

Question
What is the missing number in this pattern? 1,4,9,16,25,36,49,64,81,____1, 4, 9, 16, 25, 36, 49, 64, 81, \_\_\_\_
Get tutor helpright-arrow

Posted 1 month ago

Question
Classify the series. ∑n=012(n+2)3 \sum_{n = 0}^{12} (n + 2)^3 \newlineChoices:\newline[A]arithmetic\text{[A]arithmetic}\newline[B]geometric\text{[B]geometric}\newline[C]both\text{[C]both}\newline[D]neither\text{[D]neither}
Get tutor helpright-arrow

Posted 1 month ago

Question
Find the first three partial sums of the series.\newline1+6+11+16+21+26+⋯1 + 6 + 11 + 16 + 21 + 26 + \cdots\newlineWrite your answers as integers or fractions in simplest form.\newlineS1=S_1 = ____\newlineS2=S_2 = ____\newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 1 month ago

Question
Find the third partial sum of the series. \newline3+9+15+21+27+33+⋯3 + 9 + 15 + 21 + 27 + 33 + \cdots\newlineWrite your answer as an integer or a fraction in simplest form. \newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 1 month ago

Question
Find the first three partial sums of the series. \newline1+7+13+19+25+31+⋯1 + 7 + 13 + 19 + 25 + 31 + \cdots\newlineWrite your answers as integers or fractions in simplest form. \newlineS1=S_1 = ____\newlineS2=S_2 = ____\newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 2 months ago

Question
Does the infinite geometric series converge or diverge?\newline1+34+916+2764+⋯1 + \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots\newlineChoices:\newline[A]converge\text{[A]converge}\newline[B]diverge\text{[B]diverge}
Get tutor helpright-arrow

Posted 1 month ago

View all (37)